Отрицание – булева функция одной переменной, которая определяется следующей таблицей истинности
| х | название | обозначение | ||
| F(x) | инверсия | ⌐х, 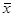 , НЕ, (NOT) , НЕ, (NOT) |
Элементарные булевы функции двух переменных приведены в следующей таблице.
| Х | название | обозначение | ||||
| y | ||||||
| F1 | Конъюнкция | х&y, x·y, x^y, min(x,y), И, (AND) | ||||
| F2 | Дизъюнкция | x 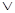 y, max(x,y),x+y, ИЛИ, (OR) y, max(x,y),x+y, ИЛИ, (OR) | ||||
| F3 | Импликация | х→у, х 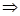 у, х у, х 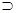 у у | ||||
| F4 | Эквивалентность | х~у, х↔у, х≡у | ||||
| F5 | Сумма по модулю 2 (исключающее ИЛИ) | х 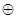 у, х+у, XOR у, х+у, XOR | ||||
| F6 | Штрих Шеффера | х|у | ||||
| F7 | Стрелка Пирса | х↓у, хºу |
Для более компактной записи сложных функций введем следующие соглашения:
1. внешние скобки опускаются;
2. сначала производятся операции в скобках;
3. считается, что приоритет связок убывает в следующем порядке: ⌐, (^,|,↓), 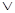 , (→,
, (→, 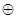 ),↔.
),↔.
Для равносильных связок (в скобках) приоритет определяется слева направо.
Задание 1. Составить таблицу истинности сложного логического выражения D = неA & (B+C). А,В, С - три простых высказывания, поэтому:
количество строк = 23 +2 = 10 (n=3, т.к. на входе три элемента А, В, С)
количество столбцов :1) А 2) В 3) С 4) не A - это инверсия А (обозначим Е) 5) B+ C это операция дизъюнкции (обозначим F) 6) D = неA & (B+C), т.е. D = E & F это операция конъюнкции
| А | В | С | E = не А(не 1) | F = В+С(2+3) | D = E&F(4*5) |
Задание 2. Составить таблицу истинности для формулы 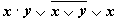 , которая содержит две переменные x и y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах - значения промежуточных формул и в последнем столбце - значение формулы. В результате получим таблицу:
, которая содержит две переменные x и y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах - значения промежуточных формул и в последнем столбце - значение формулы. В результате получим таблицу:
| Переменные | Промежуточные логические формулы | Формула | |||||
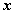 | 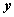 | 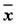 | 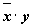 | 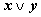 | 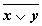 | 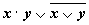 | 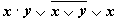 |
Из таблицы видно, что при всех наборах значений переменных x и y формула 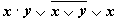 принимает значение 1, то есть является тождественно истинной.
принимает значение 1, то есть является тождественно истинной.
Задание 3. Таблица истинности для формулы 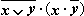 :
:
| Переменные | Промежуточные логические формулы | Формула | ||||
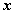 | 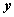 | 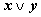 | 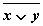 | 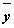 | 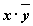 | 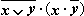 |
Из таблицы видно, что при всех наборах значений переменных x и y формула 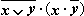 принимает значение 0, то есть является тождественно ложной.
принимает значение 0, то есть является тождественно ложной.
Задание 4. Таблица истинности для формулы 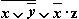 :
:
| Переменные | Промежуточные логические формулы | Формула | ||||||
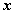 | 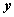 | 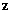 | 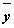 | 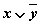 | 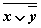 | 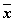 | 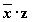 | 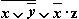 |
Из таблицы видно, что формула 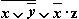 в некоторых случаях принимает значение 1, а в некоторых - 0, то есть является выполнимой.
в некоторых случаях принимает значение 1, а в некоторых - 0, то есть является выполнимой.
Задание 5. Логическое выражение 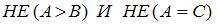 будет истинным при следующих значениях переменных А, В, С:
будет истинным при следующих значениях переменных А, В, С:
1. 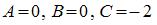
2. 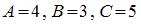
3. 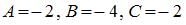
4. 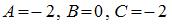
Решение: Логическое выражение 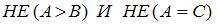 будет истинным при значениях переменных
будет истинным при значениях переменных 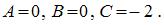 Подставив эти значения в исходное выражение, получим:
Подставив эти значения в исходное выражение, получим: 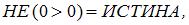
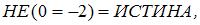
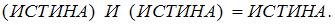 То есть значение заданного выражения истинно. При других приведенных комбинациях значений А, В, С заданное логическое выражение принимает значение ЛОЖЬ.
То есть значение заданного выражения истинно. При других приведенных комбинациях значений А, В, С заданное логическое выражение принимает значение ЛОЖЬ.
Задание 6. Логической функции F соответствует логическая схема 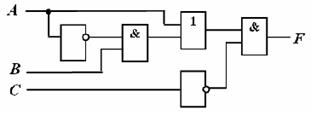
и следующая таблица истинности …
| 1. | 2. | 3. | 1. 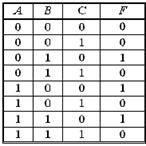 |
| 2. | 3. | 4. | 2. 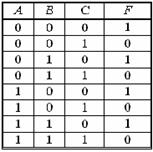 |
| 3. | 4. | 5. | 3. 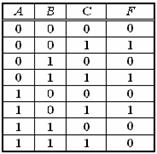 |
| 4. | 5. | 6. | 4. 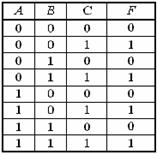 |
Задание 7. Значение 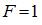 на выходе логической схемы
на выходе логической схемы 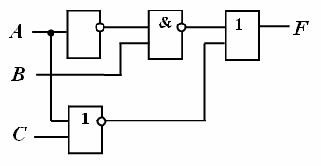
невозможно при следующей комбинации входных параметров:
1. 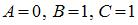
2. 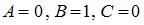
3. 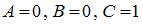
4. 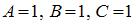
Решение: Значение 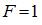 на выходе логической схемы
на выходе логической схемы

невозможно при следующей комбинации входных параметров: 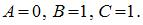 На рисунке показаны значения сигналов, формируемые логическими элементами в приведенной схеме:
На рисунке показаны значения сигналов, формируемые логическими элементами в приведенной схеме:
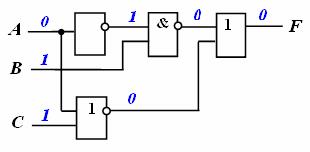
Из рисунка видно, что при комбинации входных параметров 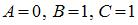 невозможнополучить значение выходного сигнала
невозможнополучить значение выходного сигнала 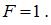 При других приведенных комбинациях А, В, С на выходе логической схемы формируется
При других приведенных комбинациях А, В, С на выходе логической схемы формируется 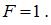
 2015-10-22
2015-10-22 1538
1538
