Изучая физическое состояние какого-либо тела, приходится наблюдать изменение его свойств от точки к точке. Каждая точка тела задается тремя координатами: x, y, z. Поэтому, изучая, скажем, распределение плотности, заключаем, что плотность тела зависит от трех переменных: x, y, z. Если физическое состояние тела к тому же еще и меняется с течением времени t, то та же плотность будет зависеть уже от значений четырех переменных: x, y, z, t.
Определение: 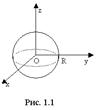 Функция двух переменных, имеет вид
Функция двух переменных, имеет вид 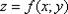 , где «икс» и «игрек» – независимые переменные. Геометрически функция двух переменных представляет собой некоторую поверхность в нашем трёхмерном пространстве. Геометрическим изображением (графиком) функции двух переменных z = f (x, y) является множество точек P (x, y, z) в трехмерном пространстве Oxyz, координаты которых удовлетворяют уравнению z = f (x, y). Так, например, (рис. 1.1) графиком функции
, где «икс» и «игрек» – независимые переменные. Геометрически функция двух переменных представляет собой некоторую поверхность в нашем трёхмерном пространстве. Геометрическим изображением (графиком) функции двух переменных z = f (x, y) является множество точек P (x, y, z) в трехмерном пространстве Oxyz, координаты которых удовлетворяют уравнению z = f (x, y). Так, например, (рис. 1.1) графиком функции 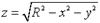 является верхняя половина сферы, а графиком функции,
является верхняя половина сферы, а графиком функции, 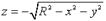 - нижняя половина сферы.
- нижняя половина сферы.
Определение: Функция трёх переменных имеет вид 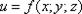 , при этом переменные
, при этом переменные 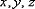 называются независимыми переменными или аргументами, переменная называется зависимой переменной или функцией. Например:
называются независимыми переменными или аргументами, переменная называется зависимой переменной или функцией. Например: 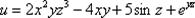 – функция трёх переменных. Функция трёх переменных подразумевает тот факт, что всё происходит в четырехмерном пространстве. График функции трёх переменных представляет собой так называемую гиперповерхность.
– функция трёх переменных. Функция трёх переменных подразумевает тот факт, что всё происходит в четырехмерном пространстве. График функции трёх переменных представляет собой так называемую гиперповерхность.
Для функции трёх переменных справедливы правила дифференцирования и таблица производных.
Частные производные. Пусть функция z = f(x,y) определена в некоторой окрестности точки М(x,y). Придадим переменной х произвольное приращение 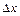 , оставляя значение переменной у неизменным. Тогда функция z = f(x,y) получит приращение
, оставляя значение переменной у неизменным. Тогда функция z = f(x,y) получит приращение 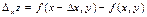 , которое называется частным приращением функции по переменной х в точке М(x,y).
, которое называется частным приращением функции по переменной х в точке М(x,y).
Аналогично определяется частное приращение функции по переменной у: 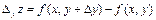 .
.
Определение: Если существует предел 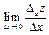
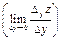 ,то он называется частной производной функции z = f(x,y) в точке М по переменной х (по переменной у) и обозначается одним из следующих символов:
,то он называется частной производной функции z = f(x,y) в точке М по переменной х (по переменной у) и обозначается одним из следующих символов: 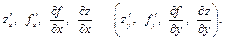
Частная производная функции двух переменных по переменной х представляет собой обыкновенную производную функции одной переменной х при фиксированном значении переменной у.
Частная производная функции двух переменных по переменной у представляет собой обыкновенную производную функции одной переменной у при фиксированном значении переменной х.
Пример 1. Найти частные производные функции 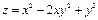
Решение: Найдем частную производную функции по переменной х, а переменную у в этом случае будем считать постоянной: 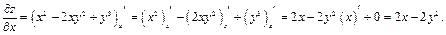
Найдем частную производную функции по переменной у, а переменную х в этом случае будем считать постоянной: 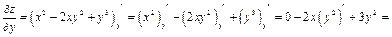
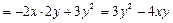 .
.
Полный дифференциал функции. Пусть функция z=f(x,y) определена в некоторой окрестности точки М(x,y). Составим полное приращение функции в точке М: 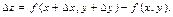
Функция z = f(x,y) называется дифференцируемой в точке М(x,y), если ее полное приращение можно представить в виде 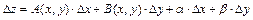 , где
, где 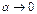 и
и 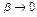 при
при 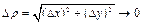 ,
, 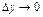 . Сумма первых двух слагаемых представляет собой главную часть приращения функции.
. Сумма первых двух слагаемых представляет собой главную часть приращения функции.
Главная часть приращения функции z = f(x,y), линейная относительно 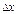 и
и 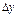 , называется полным дифференциалом функции и обозначается dz:
, называется полным дифференциалом функции и обозначается dz: 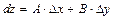 .
.
Для независимых переменных x и y полагают 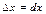 ,
, 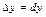 . Выражения
. Выражения 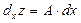 и
и 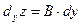 называют частными дифференциалами функции.
называют частными дифференциалами функции.
Теорема (достаточное условие дифференцируемости): Если функция z = f(x,y) имеет в некоторой окрестности точки М(x,y) непрерывные частные производные 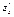 и
и 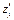 , то она дифференцируема в этой точке, причем ее полный дифференциал выражается формулой
, то она дифференцируема в этой точке, причем ее полный дифференциал выражается формулой 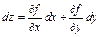 . (6)
. (6)
Пример 7. Найти полный дифференциал функции 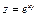 . Решение: Найдем частные производные функции
. Решение: Найдем частные производные функции 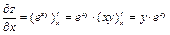 ,
, 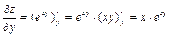 .
.
 2015-01-30
2015-01-30 13255
13255
