Вычисление собственных значений и векторов симметричной матрицы

Программа предназначена вычисление всех собственных значений и соответствующих им собственных векторов симметричной матрицы методом Якоби.

Один шаг процесса состоит в аннулировании внедиагонального элемента a_ij (i < j) матрицы

А = 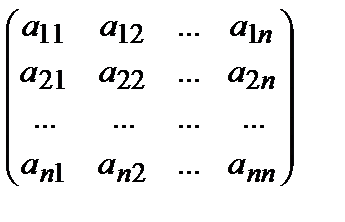, a_ij = a_ji, i, j = 1, 2, …, n,

путем преобразования вращения, которое заключается в следующем.

Вычисляются коэффициенты вращения с и s по формулам

s = , c = ,

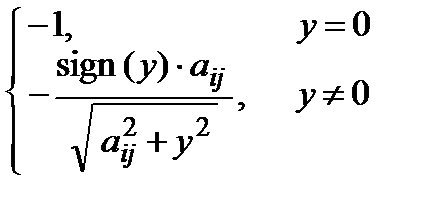где х = ; y = .

Далее, преобразуются i -й и j -й столбцы матрицы А по формулам

(11)

В преобразованной матрице элементы, стоящие на пересечении i -х и j -х строк и столбцов, преобразуются по формулам

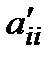= с ² a_ii + 2 сs a_ij + s ² a_jj;

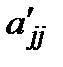= s ² a_ii – 2 сs a_ij + c ² a_jj;

= (с ² – s ²) a_ij + сs (a_jj – a_ii) ≈ 0.

По формулам (11) для всех k происходит преобразование i -й и j -й строк матрицы Т, которая первоначально является единичной.

Индексы i и j выбираются по правилу «преград». Строится последовательность чисел (так называемых преград)

, , , …, где n ₁ = .

Аннулируются все внедиагональные элементы, большие первого члена преграды. Так как в методе Якоби на месте ранее образованных нулей могут появляться числа, то процесс «проходит» по всей матрице несколько раз, пока все внедиагональные элементы не станут меньше преграды. Так до тех пор, пока все внедиагональные элементы не станут меньше числа n ₂ = · n ₁, где ε = 10 ^–р; р – желаемое число верных знаков (в программе р = 5).

В результате на диагонали матрицы А будут находиться ее собственные значения, а строки матрицы Т являются соответствующими собственными векторами.

Замечание. Исходная матрица вводится в интерактивном режиме своим нижним треугольником по строкам.

Замечание. Исходная матрица вводится в интерактивном режиме своим нижним треугольником по строкам.

П р о г р а м м а

Program IAKOBI_SZN_SV;

{программа вычисления собственных значений и}

{векторов симметричной матрицы методом Якоби}

const nmax = 50; {максимальный размер матрицы}

const eps = 1E-5; {точность вычислений}

var A: array [1..nmax] of real; {исходная матрица задается нижним треугольником}

T: array [1..nmax,1..nmax] of real; {матрица собственных векторов по строкам}

f,i,j,p,n,k,l,v,d,q,m,g:integer;

s,c,b,o,u,w,z,x,r,y:real;

label H,3,2;

Begin

writeln('программа вычисления собственных значений и');

writeln('векторов симметричной матрицы методом Якоби');

writeln;

write('введите размерность матрицы А: n=');

readln(n);

writeln('ввод матрицы А:');

for i:=1 to n do

for j:=1 to i do

Begin

write('A[',i,',',j,']=');

readln(A[round(i*(i-1)/2)+j]);

end;

for p:=1 to n do

Begin

for q:=1 to n do T[p,q]:=0;

T[p,p]:=1

end;

s:=0;

for p:=2 to n do

Begin

w:=0;

for q:=1 to p-1 do w:=w+A[round(p*(p-1)/2)+q]*A[round(p*(p-1)/2)+q];

s:=s+w;

end;

r:=sqrt(2*s);

o:=eps/n*r;

H:r:=r/n;

3:g:=0;

for q:=2 to n do

Begin

j:=round(q*(q-1)/2);

for p:=1 to q-1 do

if abs(A[j+p])>=r then

Begin

f:=round(p*(p-1)/2);

k:=f+p; l:=j+p; m:=j+q;

g:=i;

u:=A[k]; w:=A[l]; z:=A[m];

y:=(u-z)/2;

if y=0 then x:=-1 else x:=-sign(y)*w/sqrt(w*w+y*y);

s:=x/sqrt(2*(1+sqrt(1-x*x)));

c:=sqrt(1-s*s);

for i:=1 to n do

Begin

v:=round(i*(i-1)/2);

d:=v+p; if i<=p then d:=f+i;

v:=v+q; if i<=q then v:=j+i;

b:=A[d];

if i=q then goto 2;

A[d]:=b*c-A[v]*s;

2: A[v]:=b*s+A[v]*c;

b:=T[p,i]; x:=T[q,i];

T[p,i]:=b*c-x*s;

T[q,i]:=b*s+x*c

end;

x:=c*c; y:=s*s; b:=2*w*c*s;

A[k]:=u*x+z*y-b;

A[m]:=u*y+z*x+b;

A[l]:=0

End

end;

if g=i then goto 3;

if r>=o then

Begin

r:=r/n;

goto H

end;

writeln;

writeln(' Р Е З У Л Ь Т А Т Ы');

writeln;

writeln(' СОБСТ.ЗНАЧ. СОБСТВЕННЫЕ ВЕКТОРЫ');

for i:=1 to n do

Begin

writeln;

g:=g+i;

write(A[g]:10:5);

write(' ');

for j:=1 to n do

write(T[i,j]:10:5)

end;

readln;

end.

ЛАБОРАТОРНЫЕ РАБОТЫ