Порядок проведения работы

Порядок кинетостатического расчета покажем на примере.

Требуется определить давления в кинематических парах, уравновешивающую силу и момент у двигателя внутреннего сгорания с горизонтальным расположением цилиндра (см.рис.11).

Известны закон изменения внешних сил (индикаторная диаграмма) веса звеньев G₁, G₂, G₃; угловая скорость вращения звена 1; длина всех звеньев; расстояние AS₂ до центра тяжести звена 2; момент инерции шатуна относительно оси, проходящей через центр тяжести I_s2.

1) Строим планы скоростей и ускорений. Вычисляем масштабы K_w и K_v.

2) Определяем силы инерции.

Сила инерции поступательно движущегося звена 3 (поршня) равна

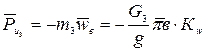[Н]

Направлена против вектора ускорения .

Силы инерции звена 2 (шатуна), совершающего сложное плоское движение, сведутся к главному вектору сил инерции Р_и2, приложенному к центру тяжести S₂ и направленному против ускорения центра тяжести, и к главному моменту сил инерции М_и2, направленному против углового ускорения Е₂.

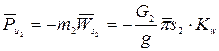
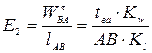
Силу Р_и2 и момент М_и2 можно привести к одной силе Р_и2, приложенной в точке К – центре качания на расстоянии h от центра тяжести. Для этого заменим момент М_и2 парой сил, равных Р_и2, с тем же моментом.

Тогда М_и2 = I_s2 · E = P_и2 · h, откуда 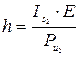. Силы Р_и2 в центре тяжести уравновесятся и останется одна приведенная сила Р_и2, приложенная в центре качания К на расстоянии h от центра тяжести.

3) Определяем давления в кинематических парах.

Начинаем с анализа последней, считая от кривошипа, присоединенного группы Асура и заканчиваем, последовательно переходя от одной группы к другой, анализом звена 1.

В нашем примере к кривошипу присоединена лишь одна группа Асура 2 класса 2 порядка 2 вида (с внешней поступательной парой).

На эту группу действует сила давления газов

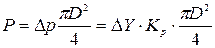
сила тяжести поршня G₃; сила инерции поршня Р_и3; сила инерции шатуна Р_и2; вес шатуна G₂ и реакция отброшенного звена R_1-2, которую разлагаем на R_1-2, перпендикулярную шатуну и Rⁿ_1-2 вдоль шатуна.

Уравнение равновесия группы под действием этих сил имеет следующий вид:

Величину и направление силы R^τ_1-2 легко найти из уравнения моментов всех сил, действующих на звено 2, относительно точки В. Если рассматривать условие равновесия звена 2, то

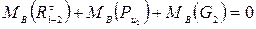
Зная R^τ_1-2, строим план сил в такой последовательности:

.

Далее, из конца вектора 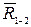проводим линию действия 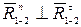, а из начала вектора 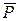- направление 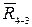по вертикали. Точка пересечения этих двух направлений и определит величины векторов 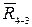и .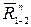

На основании плана сил легко определить величину 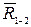и величину реакции 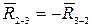. Для определения R_2-3 воспользуемся уравнением равновесия звена 3:

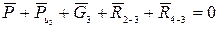
Найдем теперь точку приложения сил R_4-3, для чего, исходя из условия равенства звена 3, составим уравнение моментов относительно точки В всех сил, действующих на звено3,

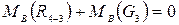; так как ,

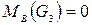то сила R_4-3 приложена в точке В.

Переходим к определению давления в шарнире 0. На звено 1 действует сила реакции 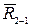отброшенного звена 2, сила веса G₁, сила реакции опоры 0 и уравновешивающая сила Р_у, проходящая вдоль линии зацепления колеса, насаженного на кривошип 1.

Уравновешивающую силу легко найти, приравняв нулю сумму моментов всех сил, действующих на кривошип 1 относительно точки 0:

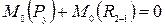
Реакцию 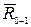можно найти, построив план сил, действующих на звено 1,

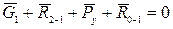
4) Определяем уравновешивающую силу R_у^' с помощью рычага Жуковского.

Строим план скоростей и в соответствующих точках прикладываем внешние силы и силы инерции, повернув их по часовой стрелке на 90⁰.

В точке а прикладываем перпендикулярно ра силу Р_у^'. Составляем уравнение равновесия рычага 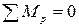и находим Р_у^':

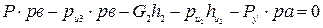
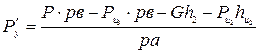
Моменты сил Р_у и Р'_у должны быть одинаковы, т.е.

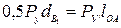
Допустимое отклонение ± 10%.