Теорема: Если требуется найти интеграл 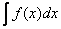 , но сложно отыскать первообразную, то с помощью замены x =
, но сложно отыскать первообразную, то с помощью замены x = 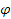 (t) и dx =
(t) и dx = 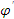 (t)dt получается:
(t)dt получается:
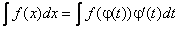
ПРИМЕР 1. Найти неопределенный интеграл:
а) Найти интеграл по свойству неопределенного интеграла 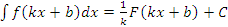
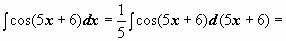
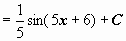
б) 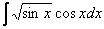 . Сделаем замену t = sinx, dt = cosxdt.
. Сделаем замену t = sinx, dt = cosxdt.
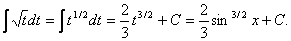
в) 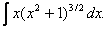 Замена
Замена 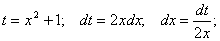 получаем:
получаем:
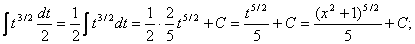
Контрольная работа №2
По дисциплине «Математика»
I курс II семестр
1 вариант
1. Вычислите пределы функции:
а) 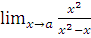 при a=2;a=0;a=
при a=2;a=0;a= 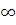
б) 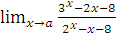 при a=-1; a=2; a=
при a=-1; a=2; a= 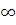
в) 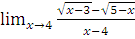 г)
г) 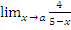 при a=-2; a=5; a=
при a=-2; a=5; a= 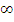
2. Найдите производные функции.
a) 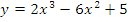 б)
б) 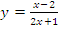 в)
в) 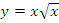 г)
г) 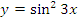
3. Найти скорость и ускорение материальной точки через (n+1)(c), где n-номер вашего варианта, если точка движется по закону S(t)= 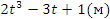
4. Составьте уравнение касательной к графику функции 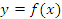 в точке с абсциссой
в точке с абсциссой 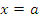 , если:
, если: 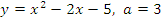
5. Исследовать функцию и построить график.
а) 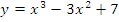 б)
б) 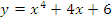
6. Решите уравнения:
а) 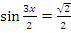
б) 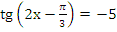
в) 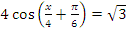
г) 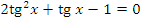
д) 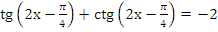
7. Вычислите неопределенные интервалы:
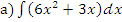 ;
;
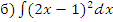 ;
;
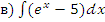 ;
;
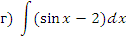
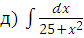 ;
;
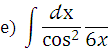
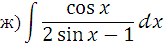
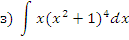
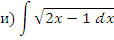
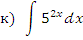
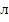 )
) 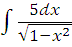
м) 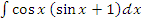
2 вариант
1. Вычислите пределы функции:
а) 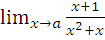 при a=-1; a=2; a=
при a=-1; a=2; a= 
б) 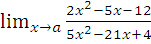 при a=-1; a=4; a=
при a=-1; a=4; a= 
в) 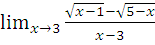 г)
г) 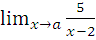 при a=-2; a=5; a=
при a=-2; a=5; a= 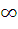
2. Найдите производные функции.
a) 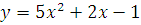 б)
б) 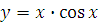 в)
в) 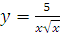 г)
г) 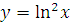
3. Найти скорость и ускорение материальной точки через (n+1)(c), где n - номер вашего варианта, если точка движется по закону S(t)= 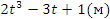
4. Составьте уравнение касательной к графику функции 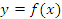 в точке с абсциссой
в точке с абсциссой 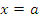 , если:
, если: 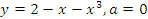
5. Исследовать функцию и построить график.
а) 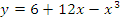 б)
б) 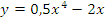
6. Решите уравнения:
а) 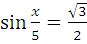
б) 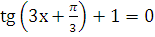
в) 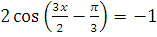
г) 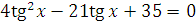
д) 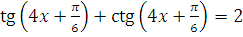
7. Вычислите неопределенные интервалы:
а) 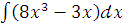 ;
;
б) 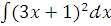 ;
;
в) 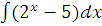 ;
;
г) 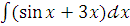
д) 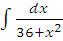 ;
;
е) 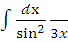
ж) 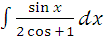
з) 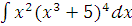
и) 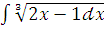
к) 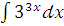
л) 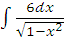
м) 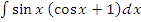
3 вариант
1. Вычислить пределы функций:
а) 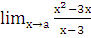 , при а=-2; а=3; а=¥;
, при а=-2; а=3; а=¥;
б) 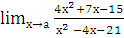 , при а=1; а=-3; а=¥;
, при а=1; а=-3; а=¥;
в) 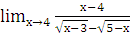 ; г)
; г) 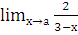 , при а=2; а=3; а=¥.
, при а=2; а=3; а=¥.
2. Найдите производные функций:
а) у= х8-5х+8; б) у= х*tgх; в) у 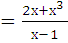 ; г) у=
; г) у= 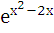 .
.
3. Найдите скорость и ускорение материальной точки через n+1 секунду, где n- номер вашего варианта, если точка движется по закону: S(t)= 2t3-3t+1(м).
4. Составьте уравнение касательной к графику функции у= f(х) в точке с абсциссой х=а, если у= х2-3х+5, а=-1.
5. Исследовать функцию и построить ее график: а) у=3х3-х+2; б) 2х4+4х-6.
6. Решить уравнение:
а) tg  =
=  ; б) Sin(
; б) Sin(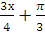 )+1=0; в) 2Cos(2х-
)+1=0; в) 2Cos(2х-  )=1; г) 2Cos2х-17Cosx-9=0;
)=1; г) 2Cos2х-17Cosx-9=0;
б) 2Sin2(2х+  )-Sin(2х+
)-Sin(2х+  )-1=0.
)-1=0.
7. Вычислите неопределенные интегралы:
а) 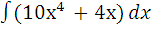
| д) 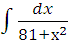
| и) 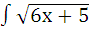 dx dx
|
б) 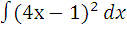
| е) 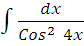
| к) 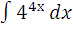
|
в) 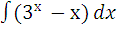
| ж) 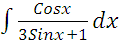
| л) 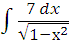
|
г) 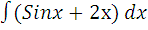
| з) 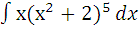
| н) 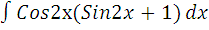
|
4 вариант
1. Вычислите пределы функции:
а) 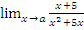 при a=3; a=5; a=
при a=3; a=5; a= 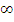
б) 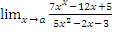 при a=--2; a=1; a=
при a=--2; a=1; a= 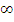
в) 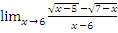
г) 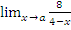 при a=2; a=4; a=
при a=2; a=4; a= 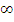
2. Найдите производные функции.
a) 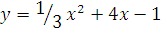 б)
б) 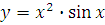 в)
в) 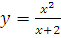 г)
г) 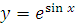
3. Найти скорость и ускорение материальной точки через (n+1)(c), где n - номер вашего варианта, если точка движется по закону S(t)= 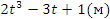
4. Составьте уравнение касательной к графику функции 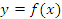 в точке с абсциссой
в точке с абсциссой 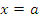 , если:
, если: 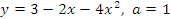
5. Исследовать функцию и построить график.
а) 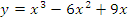 б)
б) 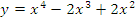
6. Решите уравнения:
а) 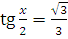
б) 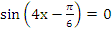
в) 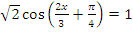
г) 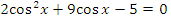
д) 
7. Вычислите неопределенные интервалы:
а) 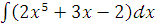 ;
;
б) 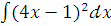 ;
;
в) 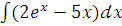 ;
;
г) 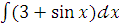
д) 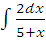 ;
;
е) 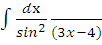
ж) 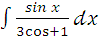
з) 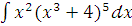
и) 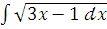
к) 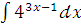
л) 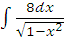
м) 
5 вариант
1. Вычислите пределы функции:
а) 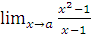 при a=2; a=1; a=
при a=2; a=1; a= 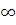
б) 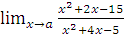 при a=2; a=-5; a=
при a=2; a=-5; a= 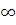
в) 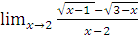
г) 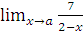 при a=-2; a=2; a=
при a=-2; a=2; a= 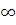
2. Найдите производные функции.
a) 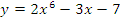 б)
б) 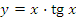 в)
в) 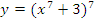 г)
г) 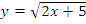
3. Найти скорость и ускорение материальной точки через (n+1)(c), где n - номер вашего варианта, если точка движется по закону S(t)= 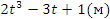
4. Составьте уравнение касательной к графику функции 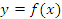 в точке с абсциссой
в точке с абсциссой 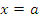 , если:
, если: 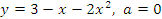
5. Исследовать функцию и построить график.
а) 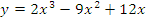 б)
б) 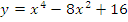
6. Решите уравнения:
а) 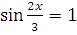
б) 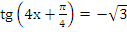
в) 2 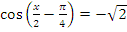
г) 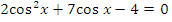
д) 
7. Вычислите неопределенные интервалы:
а) 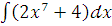 ;
;
б) 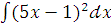 ;
;
в) 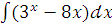 ;
;
г) 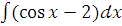
д) 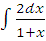 ;
;
е) 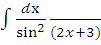
ж) 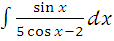
з) 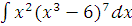
и) 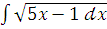
к) 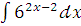
л) 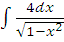
м) 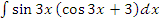
6 вариант
1. Вычислите пределы функции:
а) 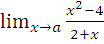 при a= -2; a=0; a=
при a= -2; a=0; a= 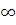
б) 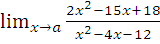 при a= -1; a=6; a=
при a= -1; a=6; a= 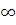
в) 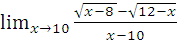
г) 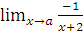 при a= -2; a=5; a=
при a= -2; a=5; a= 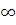
2. Найдите производные функции.
a) 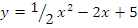 б)
б) 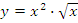 в)
в) 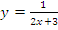 г)
г) 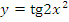
3. Найти скорость и ускорение материальной точки через (n+1)(c), где n - номер вашего варианта, если точка движется по закону S(t)= 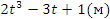
4. Составьте уравнение касательной к графику функции 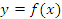 в точке с абсциссой
в точке с абсциссой 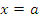 , если:
, если: 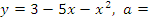
5. Исследовать функцию и построить график.
а) 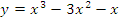 б)
б) 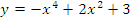
6. Решите уравнения:
а) 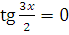
б) 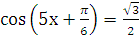
в) 2 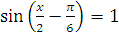
г) 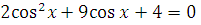
д) 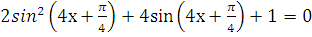
7. Вычислите неопределенные интервалы:
а) 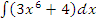 ;
;
б) 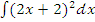 ;
;
в) 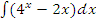 ;
;
г) 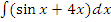 ;
;
д) 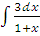 ;
;
е) 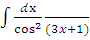 ;
;
ж) 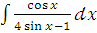 ;
;
з) 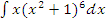 ;
;
и) 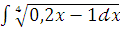 ;
;
к) 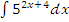 ;
;
л) 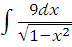 ;
;
м) 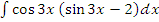
7 вариант
1. Вычислите пределы функции:
а) 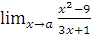 при a= -3; a=0; a=
при a= -3; a=0; a= 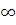
б) 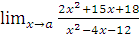 при a= -1; a=6; a=
при a= -1; a=6; a= 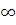
в) 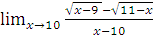
г) 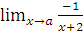 при a= -2; a=5; a=
при a= -2; a=5; a= 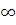
2. Найдите производные функции.
a) 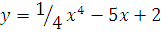 б)
б) 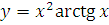 в)
в) 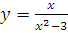 г)
г) 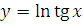
3. Найти скорость и ускорение материальной точки через (n+1)(c), где n - номер вашего варианта, если точка движется по закону S(t)= 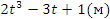
4. Составьте уравнение касательной к графику функции 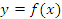 в точке с абсциссой
в точке с абсциссой 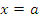 , если:
, если: 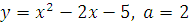
5. Исследовать функцию и построить график.
а) 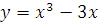 б)
б) 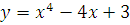
6. Решите уравнения:
а) 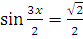
б) 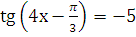
в) 2 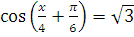
г) 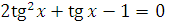
д) 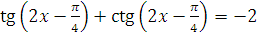
7. Вычислите неопределенные интервалы:
а) 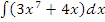 ;
;
б) 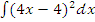 ;
;
в) 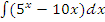 ;
;
г) 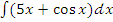
д) 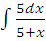 ;
;
е) 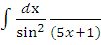
ж) 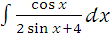
з) 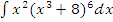
и) 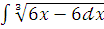
к) 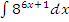
л) 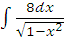
м) 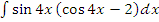
8 вариант
1. Вычислите пределы функции:
а) 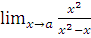 при a=2; a=0; a=
при a=2; a=0; a= 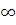
б) 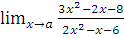 при a= -1; a=2; a=
при a= -1; a=2; a= 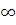
в) 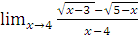
г) 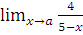 при a= -2; a=5; a=
при a= -2; a=5; a= 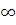
2. Найдите производные функции.
a) 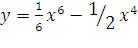 б)
б) 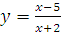 в)
в) 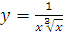 г)
г) 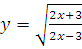
3. Найти скорость и ускорение материальной точки через (n+1)(c), где n - номер вашего варианта, если точка движется по закону S(t)= 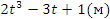
4. Составьте уравнение касательной к графику функции 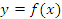 в точке с абсциссой
в точке с абсциссой 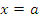 , если:
, если: 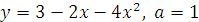
5. Исследовать функцию и построить график.
а) 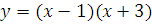 б)
б) 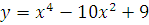
6. Решите уравнения:
а) 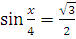
б) 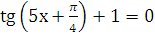
в) 2 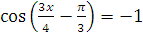
г) 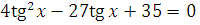
д) 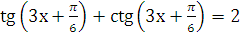
7. Вычислите неопределенные интервалы:
а) 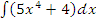 ;
;
б) 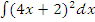 ;
;
в) 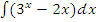 ;
;
г) 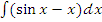
д) 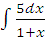 ;
;
е) 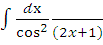
ж) 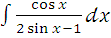
з) 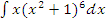
и) 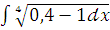
к) 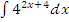
л) 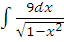
м) 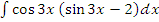
9 вариант
1. Вычислите пределы функции:
а) 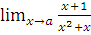 при a= -1; a=2; a=
при a= -1; a=2; a= 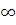
б) 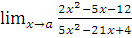 при a= -1; a=4; a=
при a= -1; a=4; a= 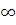
в) 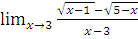
г) 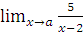 при a=-2; a=2; a=
при a=-2; a=2; a= 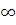
2. Найдите производные функции.
a) 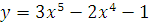 б)
б) 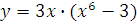 в)
в) 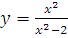 г)
г) 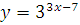
3. Найти скорость и ускорение материальной точки через (n+1)(c), где n - номер вашего варианта, если точка движется по закону S(t)= 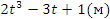
4. Составьте уравнение касательной к графику функции 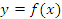 в точке с абсциссой
в точке с абсциссой 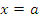 , если:
, если: 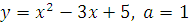
5. Исследовать функцию и построить график.
а) 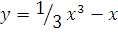 б)
б) 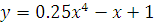
6. Решите уравнения:
а) 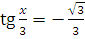
б) 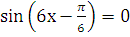
в) 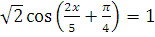
г) 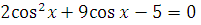
д) 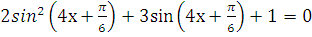
7. Вычислите неопределенные интервалы:
а) 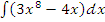 ;
;
б) 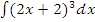 ;
;
в) 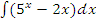 ;
;
г) 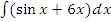
д) 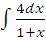 ;
;
е) 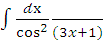
ж) 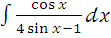
з) 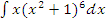
и) 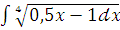
к) 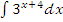
л) 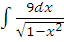
м) 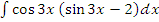
10 вариант
1. Вычислите пределы функции:
а) 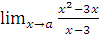 при a= -2; a=3; a=
при a= -2; a=3; a= 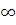
б) 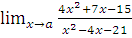 при a=1; a= -3; a=
при a=1; a= -3; a= 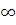
в) 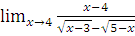
г) 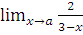 при a=2; a=3; a=
при a=2; a=3; a= 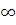
2. Найдите производные функции.
a) 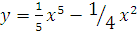 б)
б) 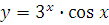 в)
в) 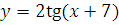 г)
г) 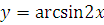
3. Найти скорость и ускорение материальной точки через (n+1)(c), где n - номер вашего варианта, если точка движется по закону S(t)= 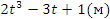
4. Составьте уравнение касательной к графику функции 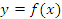 в точке с абсциссой
в точке с абсциссой 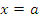 , если:
, если: 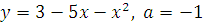
5. Исследовать функцию и построить график.
а) 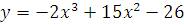 б)
б) 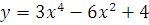
6. Решите уравнения:
а) 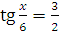
б) 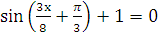
в) 2 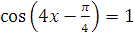
г) 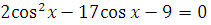
д) 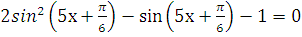
7. Вычислите неопределенные интегралы
а) 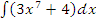 ; б)
; б) 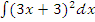 ; в)
; в) 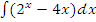 ; г)
; г) 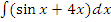
д) 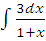 ; е)
; е) 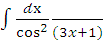 ж)
ж) 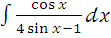 з)
з) 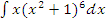
и) 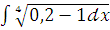 к)
к) 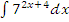 л)
л) 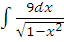 м)
м) 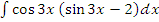
 2015-10-22
2015-10-22 568
568







