К точке а на оси ОХ аргумент может приближаться справа (х> 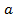 ) или (х<
) или (х< 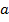 ), что обозначает соответственно как х→
), что обозначает соответственно как х→ 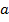 +0 или х→
+0 или х→ 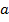 -0. Соответствующие пределы функции называются односторонними. Правосторонний предел обозначают
-0. Соответствующие пределы функции называются односторонними. Правосторонний предел обозначают 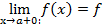 (a+0), левосторонний –
(a+0), левосторонний – 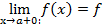 (a-0).Если
(a-0).Если 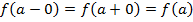 , то функция
, то функция 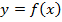 в точке а непрерывна. В противном случае в точке а функция имеет разрыв.
в точке а непрерывна. В противном случае в точке а функция имеет разрыв.
- разрыв первого рода, если оба односторонних предела в этой точке конечны и не равны, т.е. 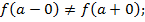
Разрыв второго рода, если хотя бы один из односторонних пределов в этой точке бесконечен или не существует.
Пример 9. Найти разрывы и нарисовать график функции
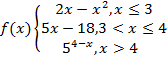
Решение. Функция 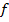 определена на всей числовой оси, составлена из элементарных функций и поэтому может иметь разрывы только в точках аналитического задания. Для х=3
определена на всей числовой оси, составлена из элементарных функций и поэтому может иметь разрывы только в точках аналитического задания. Для х=3
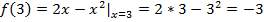 ;
;
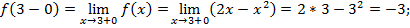
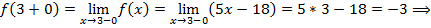
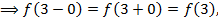
т.е. при х=3 функция непрерывна.
Для х=4
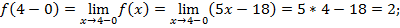
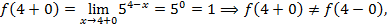
т.е. при х=4 функция имеет разрыв первого рода со скачком 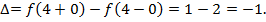
 График функций (рис. 6) состоит из параболы, прямой и графика показательной функции.
График функций (рис. 6) состоит из параболы, прямой и графика показательной функции. 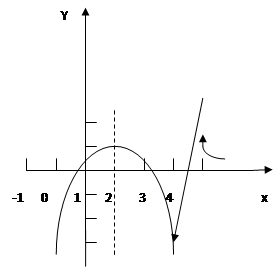 |
Рис. 6
Производная
Производной функцией f(x) в точке 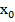 называется предел отношения приращения
называется предел отношения приращения 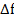 функции в этой точке к приращению
функции в этой точке к приращению 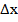 аргумента, когда последнее стремится к нулю:
аргумента, когда последнее стремится к нулю:
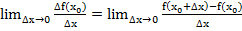 .
.
Функции f(x), имеющая производную в каждой точке некоторого промежутка, называется дифференцируемой в этом промежутке.
Основные правила дифференцирования.
Производная алгебраической суммы функций
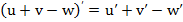 . (1)
. (1)
Производная произведения двух функций
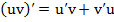 . (2)
. (2)
Производная произведения трех функций
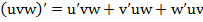 . (3)
. (3)
Производная произведения постоянной на функцию
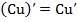 . (4)
. (4)
Производная частного (дроби)
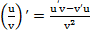 . (5)
. (5)
Частные случаи формулы (5):
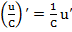 ; (6)
; (6)
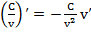 . (7)
. (7)
При условии u=x
C'=0, (8)
x'=1, (9)
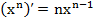 , где n-любое действительное число, (10а)
, где n-любое действительное число, (10а)
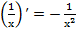 , (11a)
, (11a)
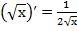 , (12a)
, (12a)
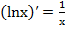 , (13a)
, (13a)
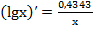 , (14a)
, (14a)
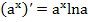 , (15a)
, (15a)
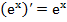 , (16a)
, (16a)
При условии 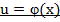
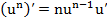 , где n-любое действительное число, (10)
, где n-любое действительное число, (10)
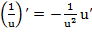 , (11)
, (11)
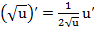 , (12)
, (12)
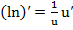 , (13)
, (13)
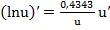 , (14)
, (14)
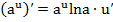 , (15)
, (15)
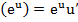 , (16)
, (16)
ПРИМЕРЫ:
1) Найти производную следующей функции:
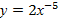
Решение: 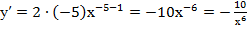
2) 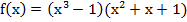
Используем формулы (2), (1), (10а), (8), (9), находим
Решение: 
3) 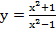
Используем формулы (5), (1), (10а), (8), получим
Решение:  .
.
4) 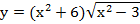
Решение: По формуле производной произведения получим:
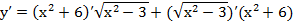 .
.
Найдем производные в каждом из слагаемых и выполним преобразования:
 .
.
Приложения производной к исследованию функций.
Функция y=f(x) называется возрастающей в промежутке a<x<b, если для любых 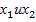 ,принадлежащих этому промежутку и таких, что
,принадлежащих этому промежутку и таких, что 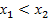 , имеет место неравенство
, имеет место неравенство 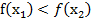 .
.
Функция y=f(x) называется убывающей в промежутке u<x<b, если для любых 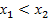 , имеет место неравенство
, имеет место неравенство 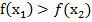 .
.
Как возрастающие, так и убывающие функции называются монотонными, а промежутки, в которых функция возрастает или убывает, - промежутками монотонности.
Возрастание и убывание функции y=f(x) характеризуется знаком ее производной: если в некотором промежутке 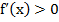 , то функция возрастает в этом промежутке; если же
, то функция возрастает в этом промежутке; если же 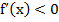 , то функция убывает в этом промежутке.
, то функция убывает в этом промежутке.
Правило нахождения экстремумов функции y=f(x) с помощью первой производной.
Найти производную f '(x).
Найти критические точки функции y=f(x), т.е. точки, в которых f '(x) обращается в нуль или терпит разрыв.
Исследовать знак производной f '(x) в промежутках, на которые найденные критические точки делят область определения функции f(x). При этом критическая точка 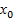 есть точка минимума, если она отделяет промежуток, в котором f '(x) < 0, от промежутка, в котором f '(x) > 0, и точка максимума – в противном случае. Если же в соседних промежутках, разделенной критической точкой
есть точка минимума, если она отделяет промежуток, в котором f '(x) < 0, от промежутка, в котором f '(x) > 0, и точка максимума – в противном случае. Если же в соседних промежутках, разделенной критической точкой 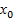 функция экстремума не имеет.
функция экстремума не имеет.
Вычислить значения функции в точках экстремума.
Исследовать на экстремум следующие функции:
ПРИМЕР:
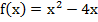
Решение: Находим 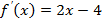 . Полагая
. Полагая 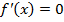 , получим единственную критическую точку ч=2. Дальнейшие рассуждения представлены в таблице:
, получим единственную критическую точку ч=2. Дальнейшие рассуждения представлены в таблице:
| x | - 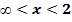 | 5/2 | 2<x< 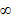 |
| f '(x) | - | 0 | + |
| f(x) | 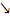 | Максимум 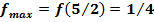 | ↗ |
|
 | |||
|
График функции 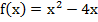 есть
есть
парабола, изображенная на рисунке. Точка минимум (2;-4) является вершиной параболы.
Правила нахождения экстремумов функции y=f(x) с помощью второй производной.
Найти производную f '(x).
Найти критические точки данной функции, в которых
f '(x)=0.
Найти вторую производную f ''(x).
Исследовать знак второй производной в каждой из критических точек. Если при этом вторая производная окажется отрицательной, то функция в такой точке имеет максимум, а если положительный, то – минимум. Если же
вторая производная ровна нулю, то экстремум функции надо искать с помощью первой производной.
Вычислить значения функции в точках экстремума.
ПРИМЕР:
Исследовать на экстремум с помощью второй производной функции:
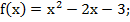
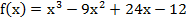 .
.
Решение: 1) Находим производную: 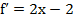 . Решая уравнение
. Решая уравнение 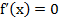 , получим критическую точку х=1. Найдем
, получим критическую точку х=1. Найдем
теперь вторую производную: 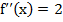 . Так как вторая производная в критической точке положительна, то при х=1 функция имеет минимум:
. Так как вторая производная в критической точке положительна, то при х=1 функция имеет минимум: 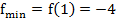 .
.
2) Находим  . Найдем теперь
. Найдем теперь 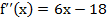 . Определим знак второй производной в критических точках. Так как
. Определим знак второй производной в критических точках. Так как 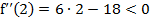 , то при х=2 функция имеет максимум; так как
, то при х=2 функция имеет максимум; так как 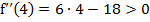 , то при х=4 функция имеет минимум. Вычислим значения функции в точках экстремума:
, то при х=4 функция имеет минимум. Вычислим значения функции в точках экстремума:  .
.
 2015-10-22
2015-10-22 1486
1486