Перепишем теперь формулу синуса двойного угла в следующем виде:
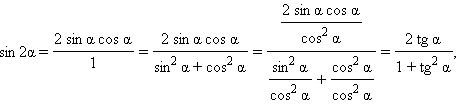 |
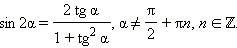 |
Аналогично можно поступить с косинусом двойного угла. Получается
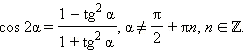 |
Разделив последнюю формулу на предпоследнюю, имеем:
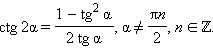 |
Последние три формулы и формулу тангенса двойного угла часто записывают в следующем виде:
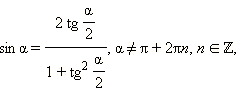 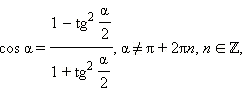 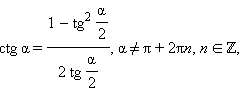 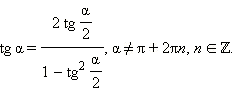 |
Эти формулы показывают, что все основные тригонометрические функции могут быть рационально выражены через 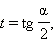 а именно:
а именно:
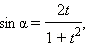 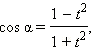 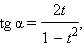 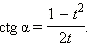 |
Говорят, что замена 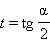 является универсальной подстановкой для основных тригонометрических функций.
является универсальной подстановкой для основных тригонометрических функций.
Формулы понижения степени
Из формулы косинуса двойного угла
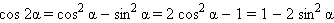 |
следуют формулы понижения степени:
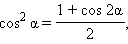 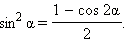 |
Формулы половинного аргумента
Если в последних формулах заменить α на 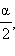 то получатся формулы половинного аргумента:
то получатся формулы половинного аргумента:
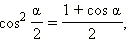 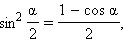 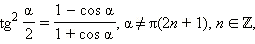 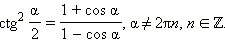 |
Можно получить немного другие формулы половинного аргумента для тангенса и котангенса. А именно:
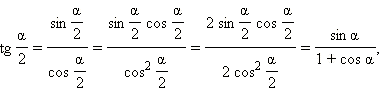 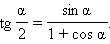 |
Совершенно аналогично получается формула
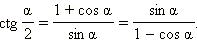 |
 2015-10-22
2015-10-22 1082
1082








