Выражение вида 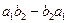 называется определителем второго порядка и обозначается:
называется определителем второго порядка и обозначается:
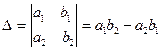 .
.
Рассмотрим систему:
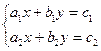 ,
,
где
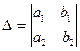 -- главный определитель,
-- главный определитель,
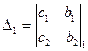 ,
, 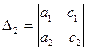 -- вспомогательные определители. Они получаются заменой в главном определителе колонки коэффициентов при х (D1) и при y (D2) колонкой свободных членов.
-- вспомогательные определители. Они получаются заменой в главном определителе колонки коэффициентов при х (D1) и при y (D2) колонкой свободных членов.
Решение системы по правилу Крамера имеет вид:
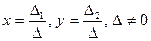 .
.
Определителем третьего порядка называется число, обозначаемое символом
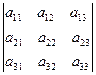
и вычисляемое по правилу Саррюса:
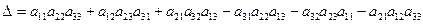 .
.




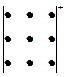
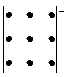
Произведение этих элементов Произведение этих элементов
берем со своими знаками берем с противоположными знаками
Для систем трех уравнений с тремя неизвестными
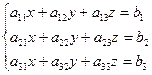
правило Крамера имеет вид:
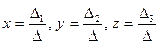 ,
,
где 
Пример (см.задание III)
Найти решение системы с помощью правила Крамера.
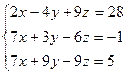
Решение.
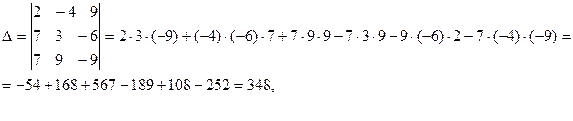
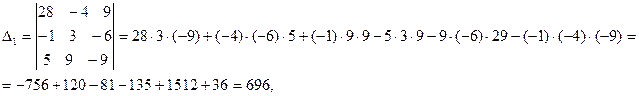
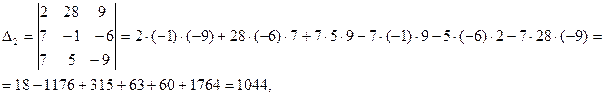
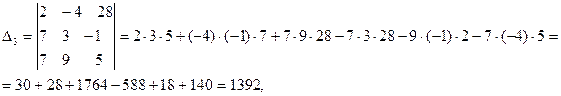
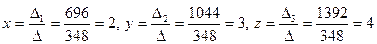 .
.
Ответ: (2, 3, 4).
ВЕКТОРНАЯ АЛГЕБРА
Векторы
Вектором называется направленный отрезок прямой или упорядоченная пара точек (про которые известно, какая первая – начало, какая вторая – конец).
Обозначают: 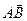 или
или 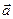 .
.
Векторы, расположенные на одной прямой или на параллельных прямых, называются коллинеарными: 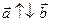 .
.
|
|
|
Если 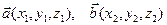 , то
, то
1) 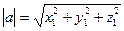 - длина вектора;
- длина вектора;
2) 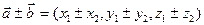 ;
;
3) 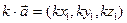 , k - число;
, k - число;
4) 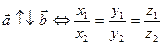 .
.
Если заданы две точки A(x1, y1, z1), B(x2, y2, z2), то
1) 
2) если 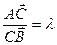 , тогда координаты точки С, делящей отрезок в заданном отношении, находится по формулам:
, тогда координаты точки С, делящей отрезок в заданном отношении, находится по формулам:
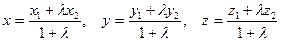
В частности, если С – середина отрезка, то
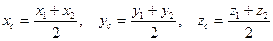 .
.
 2015-10-22
2015-10-22 256
256








