Таблица неопределённых интегралов некоторых функций.
1.) 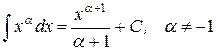
| 2.) 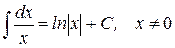
|
3.) 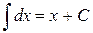
| 4.) 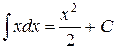
|
5.) 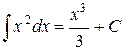
| 6.) 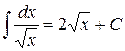
|
7.) 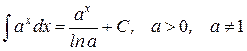
| 8.) 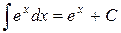
|
9.) 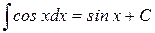
| 10.) 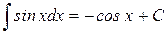
|
11.) 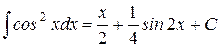
| 12.) 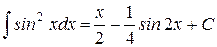
|
13.) 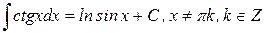
| 14.) 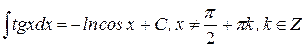
|
15.) 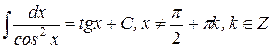
| 16.) 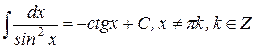
|
17.) 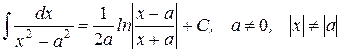
| 18.) 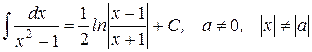
|
19.) 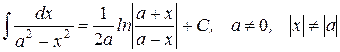
| 20.) 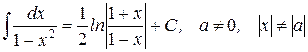
|
21.) 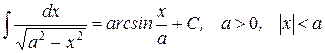
| 22.) 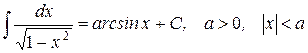
|
23.) 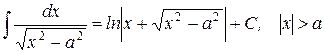
| 24.) 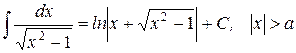
|
25.) 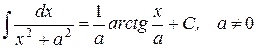
| 26.) 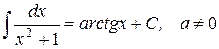
|
27.) 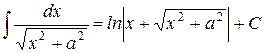
| 28.) 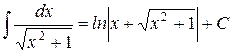
|
Основные свойства неопределённого интеграла.
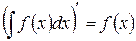
| Производная неопределенного интеграла равна подынтегральной функции. |
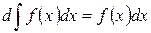
| Дифференциал от неопределенного интеграла равен подынтегральному выражению. |
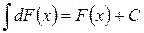
| Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной. |
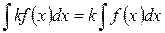
| Постоянный множитель можно вынести из-под знака интеграла, если k = const ¹0. |
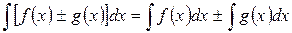
| Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций отдельно. |
Основные методы интегрирования.
| Непосредственное интегрирование | Вычисление интегралов с помощью таблицы простейших интегралов и основных свойств неопределённых интегралов. |
| Метод подстановки (метод замены переменной) | Введение новой переменной интегрирования позволяет свести нахождение данного интеграла к нахождению табличного, т. е. перейти к непосредственному интегрированию:
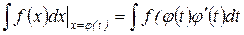 или или
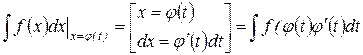
|
| Метод интегрирования по частям | Основан на использовании формулы дифференцирования произведения двух функций:
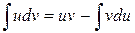
|
 2015-10-22
2015-10-22 467
467








