Дифференцирование сложной функции

Если функция х = j (t) имеет производную в точке t ₀, а функция y = f (x) имеет производную в соответствующей точке х ₀= j (t ₀), то сложная функция f (j (t)) имеет производную в точке t ₀, и имеет место следующая формула:

y ¢(t ₀)= f ¢(x ₀) j ¢(t ₀).

Задание 1. Вычислить производные следующих функций:

Задание 2. Вычислить производные следующих сложных функций:

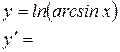
Задание 3. Вычислить производные следующих неявных функций:

Задание 4. Вычислить производные следующих функций, применяя логарифмическое дифференцирование:

Применим логарифмическое дифференцирование:

Правило Лопиталя.

Пусть функции f (x) и g (x) определены и дифференцируемы в некоторой окрестности точки а, за исключением, быть может, самой точки а и g ¢(х)¹0. Пусть в указанной окрестности точки а. Тогда, если существует предел отношения производных (конечный или бесконечный), то существует и предел , причём справедлива формула:

.

· Правило Лопиталя раскрывает неопределённости типа и .

· Правило Лопиталя может применяться многократно.

· Правило Лопиталя применяется и для х ®¥, х ®+¥, х ®-¥, х ® х ₀-0, х ® х ₀+0.

Задание 5. Вычислить предел, используя правило Лопиталя: