
Замена переменной в определённом интеграле:

| Интегрирование по частям в определённом интеграле:
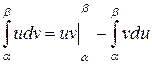
|
Связь между дифференцированием и интегрированием:
Простейшая функция

| Дифференциал
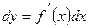
| Интеграл


|
1.) 
| 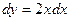
| 
|
2.) 
| 
| 
|
3.) 
| 
| 
|
4.) 
| 
| 
|
5.) 
| 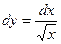
| 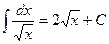
|
6.) 
| 
| 
|
7.) 
| 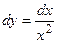
| 
|
8.) 
| 
| 
|
9.) 
| 
| 
|
10.) 
| 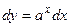
| 
|
11.) 
| 
| 
|
12.) 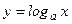
| 
| 
|
13.) 
| 
| 
|
14.) 
| 
| 
|
15.) 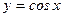
| 
| 
|
16.) 
| 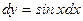
| 
|
17.) 
| 
| 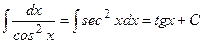
|
18.) 
| 
| 
|
19.) 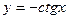
| 
| 
|
20.) 
| 
| 
|
21.) 
| 
| 
|
22.) 
| 
| 
|
23.) 
| 
| 
|
Задание 1. Найти производные и первообразные указанных функций:
| Вычислить производные следующих функций: | Вычислить одну из первообразных следующих функций: |
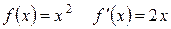
| 
|

| 
|

| 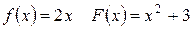
|
Вычислить все первообразные следующей функции  (вычислить неопределённый интеграл): (вычислить неопределённый интеграл):  , где С = const. , где С = const.
|
Задание 2. Вычислить неопределённые интегралы:
 , где С = const. , где С = const.
| 
| 
|
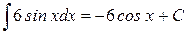 , где С = const. , где С = const.
| 
| 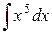
|
 , где С = const. , где С = const.
| 
| 
|
 , где С = const. , где С = const.
| 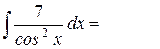
| 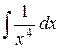
|
 , где С = const. , где С = const.
| 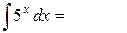
| 
|
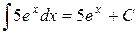 , где С = const. , где С = const.
| 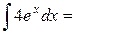
| 
|
 , где С = const. , где С = const.
| 
| 
|
Непосредственное интегрирование:
Задание 3. Вычислить неопределённые интегралы. Результаты интегрирования проверить дифференцированием:
| Интегрирование: | Дифференцирование: |
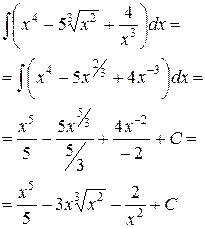
| 
|

| 
|

|
 2015-10-22
2015-10-22 329
329








