1. Производная неопределенного интеграла равна подынтегральной функции; дифференциал неопределенного интеграла равен подынтегральному выражению:
 ,
,  .
.
2. Неопределенный интеграл от дифференциала функции равен этой функции, сложенной с произвольной постоянной, т.е.
 .
.
3. Постоянный множитель можно выносить за знак неопределенного интеграла:
 .
.
4. Неопределенный интеграл от алгебраической суммы функций равен такой же алгебраической сумме неопределенных интегралов от каждой функции:
 .
.
Основные формулы интегрирования (табличные интегралы).
Из каждой формулы дифференцирования вытекает соответствующая ей формула интегрирования. Например, из того, что  , следует равенство
, следует равенство  .
.
Ниже приведена таблица основных табличных интегралов:
1. 
2. 
3. 
4. 
5. 
6. 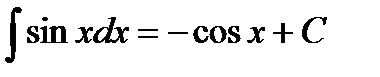
7. 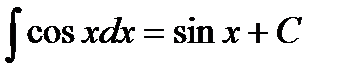
8. 
9. 
10. 
11. 
Справедливость этих формул можно проверить дифференцированием.
Непосредственное интегрирование. Под непосредственным интегрированием понимают такой способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам.
Пример 1. Найти интеграл  .
.
Решение. Воспользуемся определением степени с отрицательным показателем
(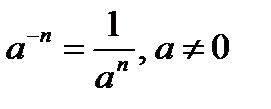 ) и найдем неопределенный интеграл от степени:
) и найдем неопределенный интеграл от степени:
 .
.
Пример 2. Найти интеграл  .
.
Решение. Воспользуемся определением степени с дробным показателем ( ) и найдем неопределенный интеграл от степени:
) и найдем неопределенный интеграл от степени:
 .
.
Пример 3. Найти интеграл  .
.
Решение. Воспользуемся определением степени с дробным показателем и правилом умножения степеней с одинаковыми основаниями ( ) и найдем неопределенный интеграл от степени:
) и найдем неопределенный интеграл от степени:
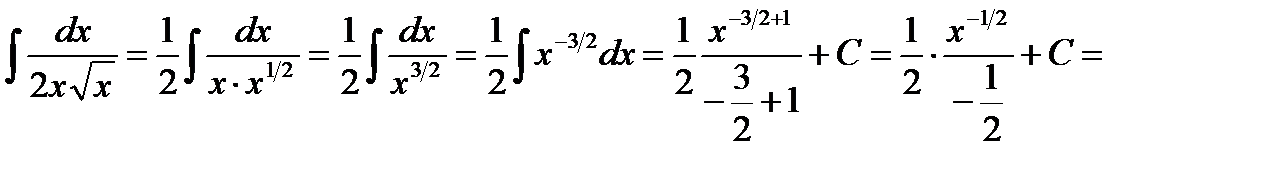

Пример 4. Найти интеграл  .
.
Решение. Воспользуемся определением степени с дробным показателем ( ), правилами действий над степенями с одинаковыми основаниями (
), правилами действий над степенями с одинаковыми основаниями ( ,
,  ), правилом деления суммы на число и найдем интеграл от каждого слагаемого отдельно. Имеем
), правилом деления суммы на число и найдем интеграл от каждого слагаемого отдельно. Имеем


Пример 5. Найти интеграл  .
.
Решение. Раскроем скобки по формуле  и неопределенный интеграл от полученной алгебраической суммы функций заменим такой же алгебраической суммой неопределенных интегралов от каждой функции:
и неопределенный интеграл от полученной алгебраической суммы функций заменим такой же алгебраической суммой неопределенных интегралов от каждой функции:
 .
.
Пример 6. Найти интеграл  .
.
Решение. Для нахождения интеграла воспользуемся формулой 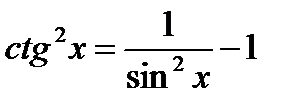 и свойствами неопределенного интеграла:
и свойствами неопределенного интеграла:
 .
.
Интегрирование методом подстановки. Если интеграл затруднительно привести к табличному с помощью элементарных преобразований, то в этом случае пользуются методом подстановки.
Сущность метода заключается в том, что путем введения новой переменной удается свести данный интеграл к новому интегралу, который сравнительно легко берется непосредственно.
Для интегрирования методом подстановки можно использовать следующую схему:
1) часть подынтегральной функции надо заменить новой переменной;
2) найти дифференциал от обеих частей замены;
3) все подынтегральное выражение выразить через новую переменную (после чего должен получиться табличный интеграл);
4) найти полученный табличный интеграл;
5) сделать обратную замену.
Пример 7. Найти интеграл  .
.
Решение. Произведем подстановку  , тогда
, тогда 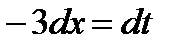 , откуда
, откуда  . Далее получаем
. Далее получаем
 .
.
Пример 8. Найти интеграл  .
.
Решение. Сначала положим  , тогда
, тогда  , откуда
, откуда  . Далее получаем
. Далее получаем

Пример 9. Найти интеграл  .
.
Решение. Положим  , тогда
, тогда  откуда
откуда  . Далее получаем
. Далее получаем
 .
.
Пример 10. Найти интеграл  .
.
Решение. Положим  , тогда
, тогда  , откуда
, откуда  . Далее получаем
. Далее получаем
 .
.
В практике интегрирования часто встречаются интегралы, для нахождения которых можно использовать следующие формулы ( ,
,  - постоянные):
- постоянные):
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
Так, при нахождении  можно использовать формулу
можно использовать формулу  , где
, где  . Тогда
. Тогда  .
.
 2015-10-22
2015-10-22 2091
2091
