Здесь используют формулу: 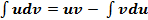
Пример11. Найти интеграл: 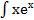 . Решение:
. Решение: 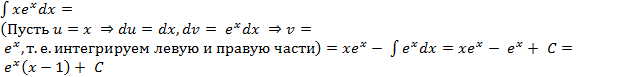
Пример12. Найдите интеграл: 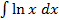 . Решение:
. Решение: 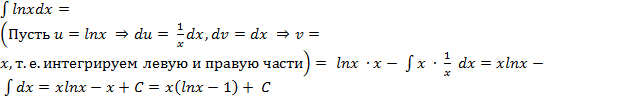
Пример 13. Найдите интеграл: 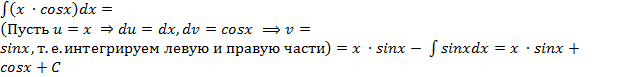
Понятие определенного интеграла. Пусть функция 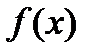 определена на отрезке
определена на отрезке 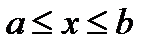 . Допустим для простоты, что функция
. Допустим для простоты, что функция 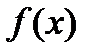 в указанном промежутке неотрицательна и
в указанном промежутке неотрицательна и 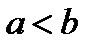 . Разобьем этот отрезок на n частей точками
. Разобьем этот отрезок на n частей точками 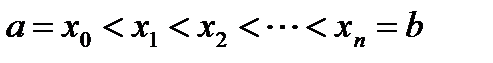 . На каждом из частичных отрезков
. На каждом из частичных отрезков 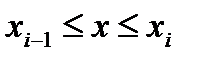 (i =1, 2, 3, …, n) возьмем произвольную точку
(i =1, 2, 3, …, n) возьмем произвольную точку 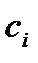 и составим сумму:
и составим сумму:
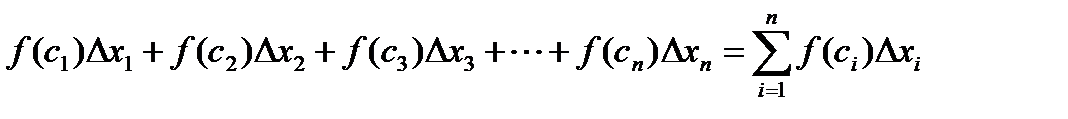 ,
,
где 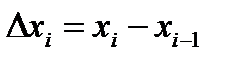 . Эта сумма носит название интегральной суммы функции
. Эта сумма носит название интегральной суммы функции 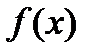 на отрезке
на отрезке 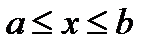 .
.
Геометрически (рис. 10) каждое слагаемое интегральной суммы равно площади прямоугольника с основанием 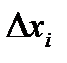 и высотой
и высотой 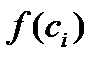 , а вся сумма равна площади «ступенчатой фигуры», получающейся объединением всех указанных выше прямоугольников.
, а вся сумма равна площади «ступенчатой фигуры», получающейся объединением всех указанных выше прямоугольников.
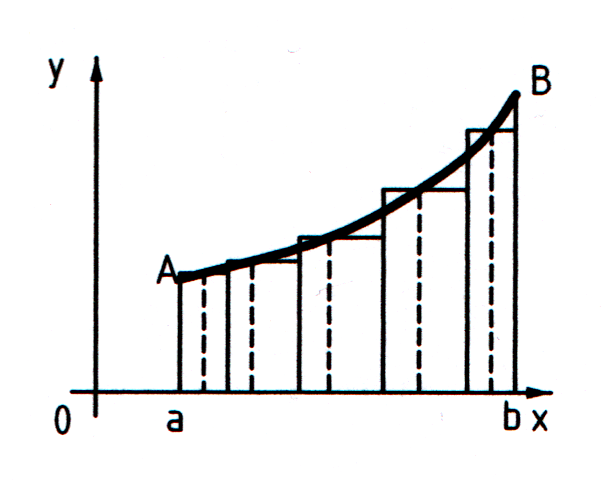
Рисунок 10
Очевидно, что при всевозможных разбиениях отрезка 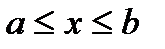 на части получим различные интегральные суммы, а, следовательно, и различные «ступенчатые фигуры».
на части получим различные интегральные суммы, а, следовательно, и различные «ступенчатые фигуры».
Будем увеличивать число точек разбиения так, чтобы длина наибольшего из отрезков 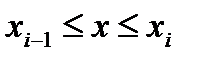 стремилась к нулю. Во многих случаях при таком разбиении интегральная сумма будет стремиться к некоторому конечному пределу, не зависящему ни от способа, каким выбираются точки деления
стремилась к нулю. Во многих случаях при таком разбиении интегральная сумма будет стремиться к некоторому конечному пределу, не зависящему ни от способа, каким выбираются точки деления 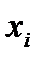 , ни от того, как выбираются точки
, ни от того, как выбираются точки 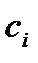 .
.
Этот предел и называется определенным интегралом от функции 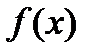 на отрезке
на отрезке 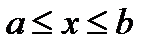 .
.
Определенным интегралом от функции 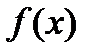 на отрезке
на отрезке 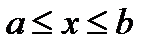 называется предел, к которому стремится интегральная сумма при стремлении к нулю длины наибольшего частичного интервала. Он обозначается символом
называется предел, к которому стремится интегральная сумма при стремлении к нулю длины наибольшего частичного интервала. Он обозначается символом 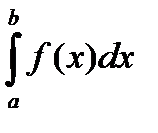 и читается «интеграл от a и b от функции
и читается «интеграл от a и b от функции 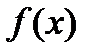 по
по 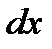 » или, короче, «интеграл от a и b от функции
» или, короче, «интеграл от a и b от функции 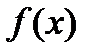
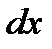 ».
».
По определению,
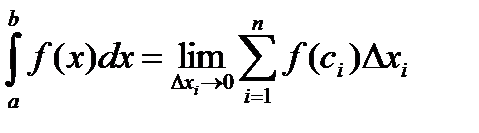 .
.
Число a называется нижним пределом интегрирования, число b – верхним; отрезок 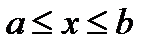 - отрезком интегрирования.
- отрезком интегрирования.
Заметим, что всякая непрерывная на отрезке 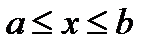 функция
функция 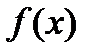 интегрируема на отрезке.
интегрируема на отрезке.
Если интегрируемая на отрезке 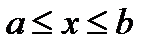 функция
функция 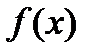 неотрицательна, то определенный интеграл
неотрицательна, то определенный интеграл 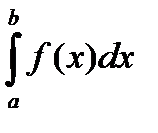 численно равен площади S криволинейной трапеции aABb, ограниченной графиком функции
численно равен площади S криволинейной трапеции aABb, ограниченной графиком функции 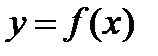 , осью абсцисс и прямыми
, осью абсцисс и прямыми 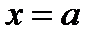 и
и 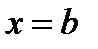 (рис. 10), т.е.
(рис. 10), т.е. 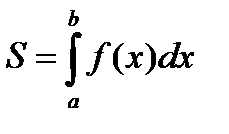 . В этом и заключается геометрический смысл определенного интеграла.
. В этом и заключается геометрический смысл определенного интеграла.
Основные свойства определенного интеграла. Все свойства сформулированы в предположении, что рассматриваемые функции интегрируемы в соответствующих промежутках.
1. Определенный интеграл с одинаковыми пределами равен нулю:
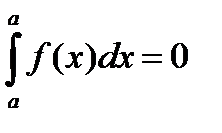
2. При перестановке пределов интегрирования знак интеграла меняется на противоположный:
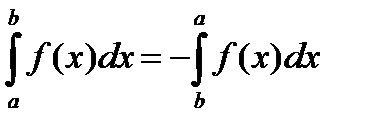 .
.
3. Отрезок интегрировании можно разбивать на части:
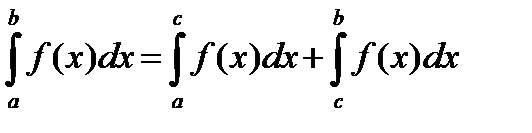 , где
, где 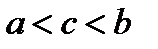
4. Постоянный множитель можно выносить за знак интеграла:
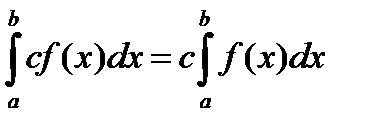
5. Интеграл от алгебраической суммы функций равен такой же алгебраической сумме интегралов от всех слагаемых:
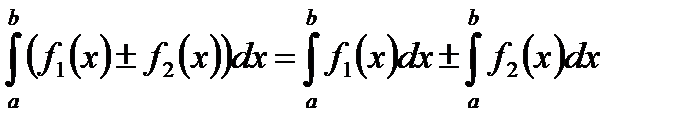
Непосредственное вычисление определенного интеграла. Для вычисления определенного интеграла, когда можно найти соответствующий интеграл, служит формула Ньютона-Лейбница
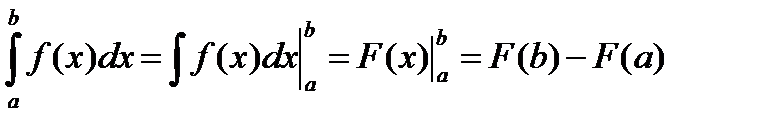 ,
,
Т.е. определенный интеграл равен разности значений любой первообразной функции при верхнем и нижнем пределах интегрирования.
Из этой формулы виден порядок вычисления определенного интеграла:
1) найти неопределенный интеграл от данной функции;
2) в полученную первообразную подставить вместо аргумента сначала верхний, затем нижний предел интеграла;
3) из результата подстановки верхнего предела вычесть результат подстановки нижнего предела.
Пример 14. Вычислить интеграл 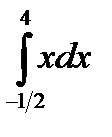 .
.
Решение. Применив указанное правило, вычислим данный определенный интеграл:
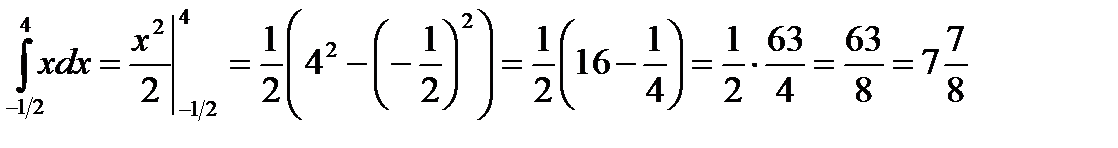
Пример 15. Вычислить интеграл 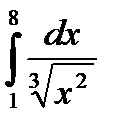 .
.
Решение. Воспользуемся определением степени с дробным и отрицательным показателем и вычислим определенный интеграл:
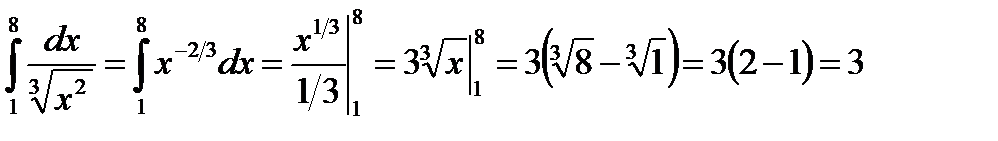
Пример 16. Вычислить интеграл 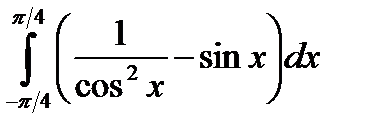 .
.
Решение. Интеграл от разности функций заменим разностью интегралов от каждой функции:
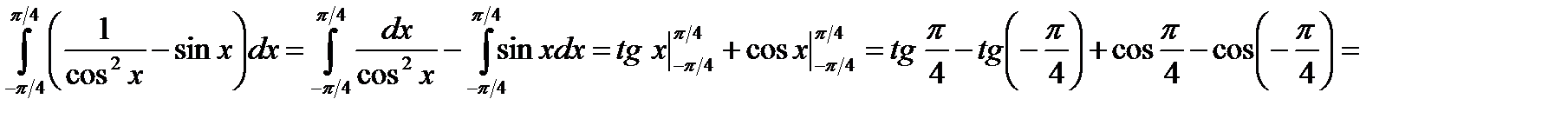
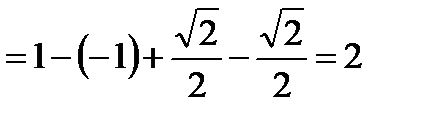 .
.
Пример 17. Вычислить интеграл 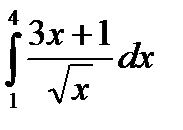 .
.
Решение. Воспользуемся определением степени с дробным показателем, правилом деления суммы на число и вычислим определенный интеграл от каждого слагаемого отдельно:
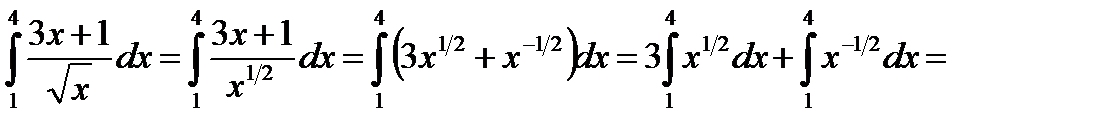
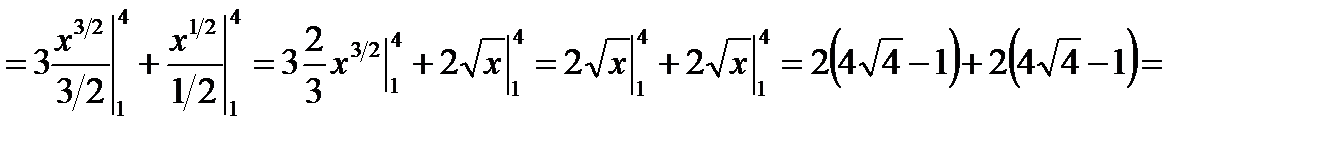
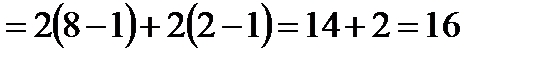
 2015-10-22
2015-10-22 1924
1924
