Вычисление определенного интеграла методом подстановки

Вычисление определенного интеграла методом подстановки состоит в следующем:

1) часть подынтегральной функции заменить новой переменной;

2) найти новые пределы определенного интеграла;

3) найти дифференциал от обеих частей замены;

4) все подынтегральное выражение выразить через новую переменную (после чего должен получиться табличный интеграл);

5) вычислить полученный определенный интеграл.

Пример 18. Вычислить интеграл .

Решение. Введем подстановку , тогда , . Определим пределы интегрирования для переменной t. При x=0 получаем , при x=7 получаем .

Выразив подынтегральное выражение через t и dt и перейдя к новым пределам, получим

.

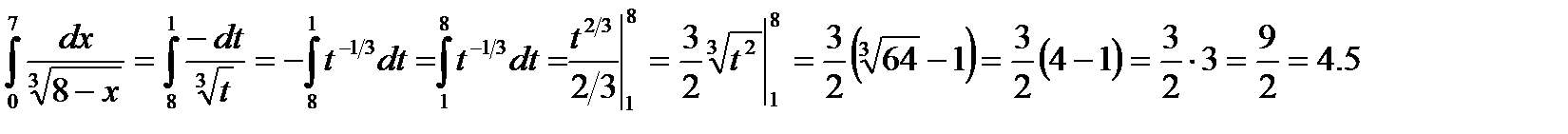Пример 19. Вычислить интеграл .

Решение. Произведем подстановку , тогда , . Определим пределы интегрирования для переменной t. При x=1 получаем , при x=2 получаем .

Выразив подынтегральное выражение через t и dt и перейдя к новым пределам, получим

.

Пример 20. Вычислить интеграл .

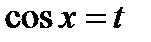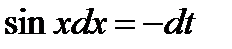Решение. Положим , тогда и . Определим пределы интегрирования для переменной t: , .

Выразив подынтегральное выражение через t и dt и перейдя к новым пределам, получим

Пример 21. Вычислить интеграл .

Решение. Пусть , , , .

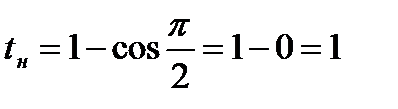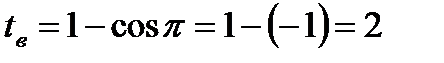Пример 22. Вычислить интеграл .

Решение. Сначала преобразуем подынтегральное выражение:

.

Затем вычислим интеграл от разности функций, заменив его разностью определенных интегралов от каждой функции:

.

Вычислим каждый интеграл отдельно:

;

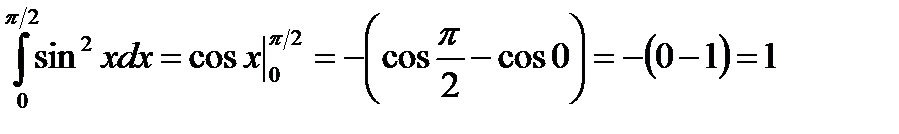Пусть , , , , .

.

Тогда