Интегральное исчисление

По данной теме ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решение примеров из данного пособия. Ответьте на вопросы и выполните упражнения для самопроверки.

Неопределенный интеграл

Понятие неопределенного интеграла. Напомним, что дифференцирование – это действие, с помощью которого по данной функции находится ее производная или дифференциал. Например, если 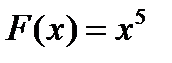, то , .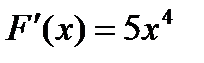

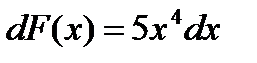Как мы знаем, нахождение производной имеет большое практическое значение. Так, по данному закону движения тела 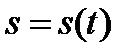мы путем дифференцирования находим скорость 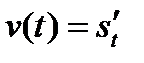, а затем и ускорение 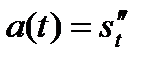по данному уравнению кривой 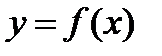определяем угловой коэффициент касательной, проведенной к этой кривой: .

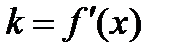На деле, однако, часто приходится решать обратную задачу: по известной скорости движения тела устанавливать закон его движения, по данному угловому коэффициенту касательной к кривой находить уравнение кривой и т.п. иначе говоря, по данной производной отыскивать функцию, от которой найдена эта производная, т.е. выполнять действие обратное дифференцированию. Это действие называется интегрированием. С помощью интегрирования по данной производной или дифференциалу функции находится сама функция. Например, если , то 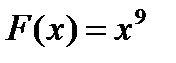, так как .

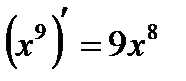Дифференцируемая функция 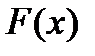, 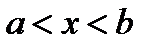называется первообразной для функции 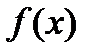на интервале 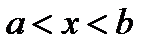, если 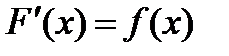для каждого .

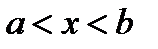Так, для функции 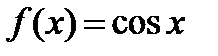первообразной служит функция 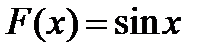, поскольку .

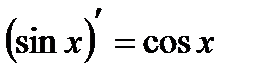Для заданной функции ее первообразная определяется неоднозначно.

Справедливо теорема: если 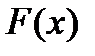- первообразная для 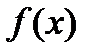на некотором промежутке, то и функция 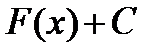, где C – любая постоянная, также является первообразной для функции 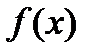на этом промежутке. Обратно: каждая функция, являющаяся первообразной для 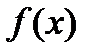в данном промежутке, может быть записана в виде .

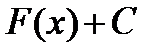Значит, достаточно найти для данной функции 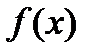только одну первообразную функцию 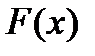, чтобы знать все первообразные, так как они отличаются друг от друга только на постоянную величину.

Совокупность 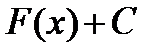всех первообразных функций 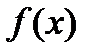на интервале 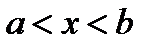называют неопределенным интегралом от функции 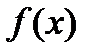на этом интервале и пишут 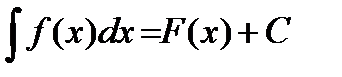. Здесь 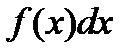- подынтегральное выражение; 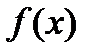- подынтегральная функция; x – переменная интегрирования; C – произвольная постоянная.

Например, 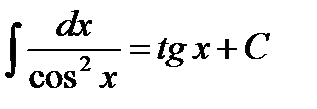, так как .

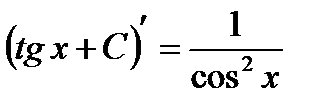Если функция 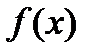имеет на некотором промежутке хотя бы одну первообразную, то ее называют интегрируемой на этом промежутке. Можно доказать, что любая функция, непрерывная на отрезке 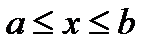, интегрируема на этом отрезке.