Решение систем линейных уравнений

1. Матричный метод.

Пусть имеется система – го порядка

Матрица – матрица системы;

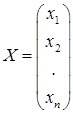– столбец неизвестных; 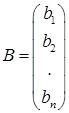– столбец свободных членов.

Данная система эквивалентна матричному уравнению: , тогда решение системы эквивалентно решению указанного матричного уравнения т.е. .

2. Правило Крамера.

Если определитель системы линейных уравнений с неизвестными отличен от нуля, то эта система имеет единственное решение, которое может быть найдено по формулам

, где – определитель, полученный из главного заменой – го столбца столбцом свободных членов.

Замечание: а) Если , а какой-либо из , то, очевидно, что система решений не имеет.

б) Если все определители одновременно равны нулю, то система либо имеет бесчисленное множество решений, либо несовместна.

3. Метод Гаусса (метод исключения неизвестных).

Пусть дана произвольная система линейных уравнений

Расширенной матрицей системы назовем матрицу полученную из А добавлением столбца свободных членов .

Под элементарными преобразованиями системы линейных уравнений понимаются следующие операции:

1. Умножение какого-либо уравнения системы на число, отличное от нуля;

2. Прибавление к одному уравнению другого уравнения, умноженного на произвольное число;

3. Перемена местами двух уравнений в системе.

Очевидно, что каждому элементарному преобразованию системы соответствует аналогичное преобразование строк расширенной матрицы этой системы и наоборот.

Элементарные преобразования системы обратимы, т.е. если мы, сделав элементарное преобразование, перешли от одной системы к другой, то можем вернуться к первоначальной, выполнив некоторое другое преобразование.

Определение: две системы линейных уравнений от одних и тех же переменных называются равносильными, если каждое решение одной из них является решением другой, и наоборот (или лбе системы несовместны).

При элементарных преобразованиях система переходит в равносильную систему.

Метод Гаусса заключается в том, что при помощи элементарных преобразований систему (расширенную матрицу) приводят к трапециевидной форме. После этого уже не представляет труда разобраться в вопросе о совместности системы, определить число решений и найти сами решения.