Векторы и действия с ними

Вектором назовем направленный отрезок в пространстве. Обозначения: . Длина отрезка AB является длиной вектора . Нулевой вектор – вектор имеющий нулевую длину.

Векторы коллинеарны, если они лежат на одной прямой или на параллельных прямых. Векторы компланарны, если они лежат в одной плоскости, или в параллельных плоскостях.

Два вектора называются равными, если они

a) коллинеарны,

b) одинаково направлены,

c) имеют равные длины.

Из определения следует, что вектор можно переносить параллельно самому себе в любую точку пространства. Такой вектор называется свободным.

Пусть даны два вектора . Построим равные им векторы . Тогда вектор называется суммой векторов . .

Этот способ называется «правило треугольника». Векторы можно складывать и по «правилу параллелограмма» (см рис.)

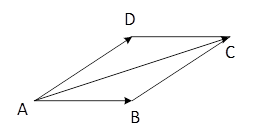
Разностью двух векторов называется сумма векторов . Вычитание действие обратное сложению

Произведение вектора на число называется вектор :

а)

б) коллинеарен

в) одинаково направлены, если и противоположно направлены, если .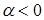

Выражение 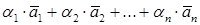называется линейной комбинацией векторов.

Базисом в пространстве называются три любых не компланарных вектора, взятые в определенном порядке.

Базисом на плоскости называются два любых не коллинеарных вектора, взятых в определенном порядке.

Если - базис в пространстве, то коэффициенты разложения вектора по базису называются координатами

Каждый вектор в плоскости может быть единственным образом разложен по данному базису этой плоскости;

Каждый вектор пространства может быть единственным образом разложен по данному базису в пространстве.

Равные векторы имеют равные координаты.

При умножении вектора на число все его координаты умножаются на это число.

При сложении векторов складываются их координаты.

Прямоугольная декартова система координат.

Прямоугольной декартовой системой координат в пространстве называется точка и базис, векторы которого

а) попарно перпендикулярны (ортогональны),

б) .

Точка называется началом координат. Прямые, проходящие через начало координат в направлении базисных векторов, называются осями координат (абсцисса, ордината, аппликата).

Приняты обозначения: .

Координаты радиус-вектора точки M называются координатами точки M в данной системе координат.

Нетрудно проверить, что координаты точки в декартовой прямоугольной системе координат по абсолютной величине равны расстоянию от этой точки до координатных плоскостей. Они имеют знак (+) или (–) в зависимости от того в каком квадранте пространства она находится.

Пусть в данной прямоугольной декартовой системе координат вектор . Найти длину вектора можно по формуле

.

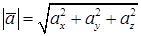Для того чтобы найти координаты вектора нужно из координат конца вычесть координаты начала.

Пусть даны точки и , тогда координаты вектора

Пусть даны концы отрезка точки , и точка и делящая его в отношении . Тогда координаты точки вычисляются по формулам ; ; .

Следствие: Координаты середины отрезка равны среднему арифметическому координат концов отрезка.

; ; .

Пусть в данной прямоугольной декартовой системе координат даны векторы

, , причем векторы сами образуют базис. Вектор можно разложить по базису т.е. записать в виде

.

Таким образом, решение задачи сводится к решению системы линейных уравнений

.