2015-10-22
627
Под углом между векторами мы понимаем угол между векторами, равными данным и имеющим общее начало. Если нет ни каких указаний, то углом между векторами считается тот, который меньше 
.
Скалярным произведением двух не нулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
Признак перпендикулярности векторов: скалярное произведение не нулевых векторов равно нулю тогда и только тогда, когда векторы перпендикулярны
.
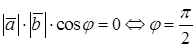т.к. 
Скалярное произведение может быть вычислено, если известны координаты веторов: 
. Скалярное произведение равно сумме произведений одноименных координат.
С помощью скалярного произведения вычисляют угол между векторами 
.
Упорядоченная тройка некомпланарных векторов называется право ориентированной или правой тройкой векторов, если из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки. В противоположном случае тройка называется левой.
Пусть даны векторы 
. Построим вектор 
, удовлетворяющий условиям:
a) 
;
b) 
;
c) 
образуют правую тройку векторов.
Вектор называется векторным произведением
векторов 
. 
.
антикоммутативность (следует из определения)
Геометрический смысл векторного произведения: 
- численно равен площади параллелограмма, построенного на векторах 
.
Векторное произведение не нулевых векторов равно нулю тогда и только тогда, когда векторы коллинеарны.
,
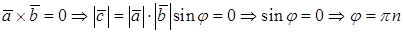т.е. векторы коллинеарны.
Смешанное произведение векторов.
Число 
называется смешанным произведением векторов иобозначается 
.
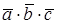Геометрический смысл: смешанное произведение не компланарных векторов равно по модулю объему параллелепипеда построенных на этих векторах. Смешанное произведение положительно, если векторы образуют правую тройку векторов, и отрицательно, если векторы образуют левую тройку векторов.
Знак смешанного произведения совпадает со знаком 
. Если векторы 
лежат по одну сторону плоскости 
, то 
и тройка векторов – правая; если векторы лежат по разные стороны плоскости , то 
и ройка векторов – левая.
Смешанное произведение не нулевых векторов равно нулю тогда и только тогда, когда векторы компланарны.
При перестановке множителей в смешанном произведении абсолютная величина числа не меняется, быть может, изменится, только знак
Смешенное произведение векторов равно определителю третьего порядка, составленному из координат векторов.
