Плоскость в пространстве

В прямоугольной декартовой системе координат каждая плоскость может быть задана линейным уравнением вида: 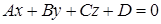, которое называется «общее уравнение»

Уравнение плоскости, проходящей через заданную точку перпендикулярно заданному вектору, имеет вид .

Геометрический смысл коэффициентов при неизвестных уравнения общего уравнения плоскости – координаты нормального вектора плоскости.

Если плоскость проходит через заданную точку компланарно двум векторам , то уравнение плоскости можно написать так: , раскрывая определитель, получим уравнение плоскости.

Если плоскость проходит через три заданные точки , то уравнение плоскости получим из условия

Если плоскость отрезает на координатных осях не нулевые отрезки т.е. пересекает координатные оси в точках , то получим уравнение плоскости в отрезках

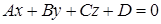Расстояние от точки до плоскости можно вычислить по формуле

.

Пусть даны две плоскости и .

а) если плоскости пересекаются, то их нормальные векторы и не коллинеарны, т.е. или .

б) если плоскости параллельны (но не совпадают), то , то

.

в) если плоскости совпадают, то .