Первообразная функция и неопределенный интеграл
Функция F(х) называется первообразной функцией для функции f(x) на промежутке X, если в каждой точке х этого промежутка
F '(x) = f(x) (т.е. производная от первообразной равна самой функции).
Например, F(x) = х3/3 является первообразной для функции
f(x) = х2, так как (х3/3)` = х2.
Отметим, что для каждой функции ее первообразная определена неоднозначно. Например, для функции f(x) = х2 первообразными являются функции F1(x) = х3/3 + 7, F2(x) = х3/3 - 10 и вообще любая функция вида
F(x) = х3/3 + С, где С – некоторая константа. В этом легко убедиться, если взять производные этих функций (производная константы равна нулю).
Аналогично в общем случае, если F(x) - некоторая первообразная для f(x), то, поскольку ((F(x) + C) ' = F '(х) = f(x), все функции вида F(x) + C, где С - произвольное число, также являются первообразными для f(x).
Из изложенного пока не ясно, можно ли описать в виде F(x) + C все первообразные для заданной функции f(x) (может быть, существуют и другие первообразные, которые нельзя представить в виде суммы найденной первообразной и константы).
Теорема. Если F1(x) и F2(х) — первообразные для функции f(x), то найдется такое число С, что будет справедливо равенство F2(x) = F1(x) + C.
Доказательство.
(F2(x) – F1(х))' = F2'(x) – F1'(х) = f(x) - f(x) = 0
По следствию из теоремы Лагранжа если производная функции равна нулю на некотором промежутке, то функция тождественно постоянна на этом промежутке. Следовательно, разность между этими первообразными будет представлять собой константу С: F2(x) – F1(х) = С Û F2(x) = F1(x) + C.
Из данной теоремы следует, что выражением F(x) + C заданы все возможные первообразные для f(x).
Совокупность всех первообразных для функции f(x) на промежутке X называется неопределенным интегралом от функции f(x) и обозначается
ò f(x)dx, где ò - знак интеграла, f(x) - подынтегральная функция, f(x)dx - подынтегральное выражение. Таким образом, ò f(x)dx = F(x) + C.
Операция нахождения неопределенного интеграла от некоторой функции называется интегрированием этой функции.
Можно доказать, что достаточным условием интегрируемости функции на промежутке X является непрерывность этой функции на данном промежутке (в то время как для для дифференцируемости функции ее непрерывность является лишь необходимым, но недостаточным условием).
Свойства неопределенного интеграла
Рассмотрим без доказательства основные свойства неопределенного интеграла.
1. Производная от неопределенного интеграла равна подынтегральной функции, т.е. (ò f(x)dx)` = f(x).
2. Дифференциал неопределенного интеграла равен подынтегральному выражению, т.е. d(ò f(x)dx) = f(x)dx.
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.
ò dF(x) = F(x) + C.
Сравнивая между собой свойства 2 и 3, можно сказать, что операции нахождения неопределенного интеграла и дифференциала взаимнообратны (знаки d и ò взаимно уничтожают друг друга, в случае свойства 3, правда, с точностью до постоянного слагаемого).
4. Постоянный множитель можно выносить за знак интеграла, т.е.
ò C*f(x)dx = C*ò f(x)dx.
5. Интеграл от алгебраической суммы двух функций равен сумме интегралов от этих функций, т.е. ò (f1(x) + f2(x))dx = ò f1(x)dx + ò f2(x)dx (это свойство остается справедливым для любого конечного числа слагаемых).
Список («таблица») основных интегралов
Перечислим интегралы от элементарных функций, которые иногда называют табличными:

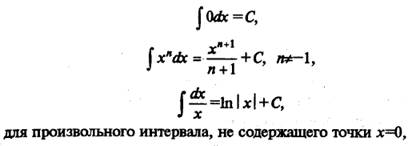
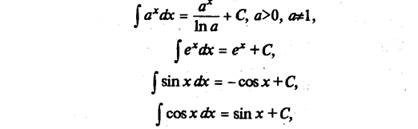
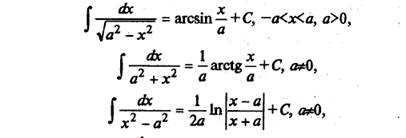
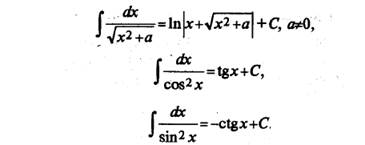
Любую из приведенных выше формул можно доказать, взяв производную от правой части (в результате будет получены подынтегральная функция).
 2015-10-22
2015-10-22 1235
1235
