Объем цилиндрического тела, ограниченного сверху непрерывной поверхностью  , снизу плоскостью
, снизу плоскостью  и сбоку цилиндрической поверхностью, с образующей параллельной оси Oz вырезающей на плоскости xOy область D, вычисляется по формуле:
и сбоку цилиндрической поверхностью, с образующей параллельной оси Oz вырезающей на плоскости xOy область D, вычисляется по формуле:

 В частности, если
В частности, если  , объем цилиндрического тела численно равен площади области D:
, объем цилиндрического тела численно равен площади области D:

Пример 1. Вычислить  где D–треугольник с вершинами O (0;0); A (1;1); B (2; 0).
где D–треугольник с вершинами O (0;0); A (1;1); B (2; 0).

|
 Выбираем (2) способ:
Выбираем (2) способ: 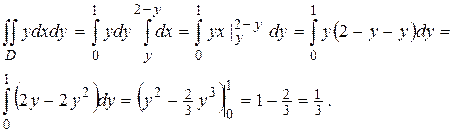
 Пример 2.
Пример 2.
Вычислить  область D – прямоугольник, ограниченный прямыми
область D – прямоугольник, ограниченный прямыми 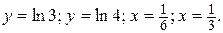
Решение.Здесь порядок интегрирования диктует подынтегральная функция, которая легче интегрируется по x, значит, внутренний интеграл будет по x:


Пример 3. Нарисовать тело, объем которого описывается интегралом  . Объем вычислить.
. Объем вычислить.
Решение. Основание тела, область D, описывается неравенствами  , сверху тело ограничено поверхностью
, сверху тело ограничено поверхностью  . Делаем чертежи. Область D:
. Делаем чертежи. Область D:  и
и  – половины парабол,
– половины парабол, 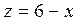 – плоскость, параллельная оси Oy, на плоскости хOy (
– плоскость, параллельная оси Oy, на плоскости хOy ( ) оставляет след
) оставляет след  . Тело, объем которого V, изображен на рисунке:
. Тело, объем которого V, изображен на рисунке:
 |

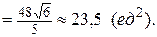
 2015-10-22
2015-10-22 2892
2892







