Интегрировани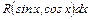е тригонометрических функций

Интегралы вида в общем случае вычисляются подстановкой 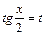. При этом

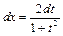, , (12)

и подынтегральная функция станет рациональной функцией от .

Пример 10. Вычислить интеграл

.

Делая подстановку 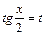и используя формулы (12), интеграл запишем в виде:

Интегралы вида 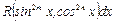, где 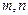- целые числа, удобно вычислять подстановкой .

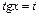Интегралы вида 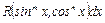, где - числа разной четности, вычисляются подстановкой 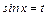, если 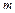четно и 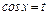, если 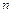четно.

Интегралы вида 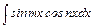; ; 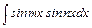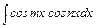, где 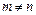, вычисляются с использованием формул тригонометрии, преобразующих произведение тригонометрических функций в их сумму.