2015-10-22
334
Пусть две дифференцируемые функци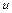и 
и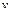 
зависят от 
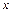. Тогда
.
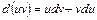Интегрируя обе части равенства, получим:
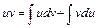
или
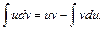(4)
Формула (4) называется формулой интегрирования по частям и применяется тогда, когда, например, интеграл в левой части равенства вычислить сложнее, чем интеграл в правой части равенства.
Пример 4. Вычислить интеграл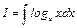 
. Обозначим: 
, 
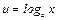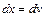. Тогда:
, 
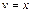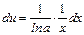. По формуле (4) получаем:
.
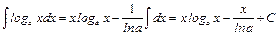Пример 5. Вычислить интеграл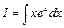 
. Обозначим: 
, 
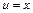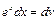. Тогда:
, 
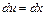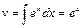. По формуле (4) получаем:
.
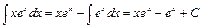При интегрировании по частям важно правильно выделить функцию 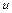в подынтегральной функции.
