2015-10-22
274
Суть метода Гаусса состоит в преобразовании системы (1) к равносильной ей системе с верхнетреугольной матрицей (прямой ход), из которой затем последовательно (обратным ходом) получаются значения всех неизвестных.
Рассмотрим прямой ход. Шаг k =1. Подвергнем систему (1) следующему преобразованию. Считая, что 
(ведущий элемент), разделим на негокоэффициенты первого уравнения, получим:
 ,
| (2) |
где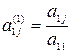 
и 
С помощью уравнения (2) исключим во всех уравнениях системы (1), начиная со второго, слагаемые, содержащие х 1. Для этого умножаем обе части уравнения (2) последовательно на а 21, а 31,…, а n1 и вычитаем соответственно из второго, третьего, …, n -го уравнения системы (1).
Тогда матрица системы будет иметь вид: 
(× - ненулевые элементы)
Далее будем работать (не трогая первого уравнения) с полученной системой:
где 
.
Шаг k =2,3, … n -1. Аналогично преобразуем полученную систему, в результате этого преобразования получим систему с верхнетреугольной матрицей с единицами по диагонали, которая эквивалентна системе (1) и легко решается:
|
|
|
  ,
| 33) |
где на k -ом шаге элементы матрицы рассчитываются по формулам:
 и  , 
 ,
| (4) |
причем 
Обратный ход. Из последнего уравнения находим xn, подставляя xn в предпоследнее уравнение, найдем xn -1, затем xn -2 и т. д. до x 1, которое находим из первого уравнения системы, когда уже известны 
, в результате получаем рекуррентные формулы для поиска решения:
|
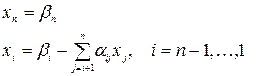
где коэффициенты 
и правые части 
,i= 1.. n – коэффициенты матрицы (3), обозначенной как 
.
Пример 1. Решить систему линейных уравнений 
, заданную матрицами 
и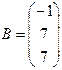 
, методом Гаусса найти det A.
Для проведения прямого хода метода Гаусса воспользуемся схемой (6) и результаты вычислений оформим в виде схемы:
| k | i | j | Вычисления | |
| ||||
| ||||
| ||||
| ||||
| ||||
| После первого шага получена матрица | 
| |||
| ||||
| ||||
| ||||
| ||||
| После второго шага получена матрица | 
| |||
| ||||
| ||||
| После третьего шага получили окончательный вид матрицы |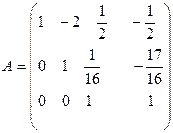 
| |||
Итак, определитель равен -9. В результате обратного хода найдем по рекуррентным формулам решение системы
, 
, 
Получили решение 
.
Схема единственного деления может использоваться также и для вычисления элементов матрицы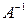 
, обратной для невырожденной матрицы А. Способ получают из определения 
, где Е — единичная матрица. Искомую матрицу 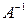и единичную матрицу представляют в виде совокупности векторов-столбцов:
|
|
|
,
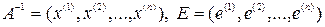тогда соотношение предстает в виде совокупности из п систем линейных алгебраических уравнений вида
| (8) |
Решение каждой системы дает соответствующий столбец обратной матрицы.
