1. Напишите программу, в которой по известной начальной скорости V и времени полета тела Т определяется угол а, под которым тело брошено по отношению к горизонту. Воспользуйтесь соотношением  .
.
2. Для тела, брошенного под углом α к горизонту с начальной скоростью V, определите дальность полета тела L (воспользуйтесь соотношением 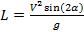 ).
).
3. Написать программу, в которой по максимальной высоте подъема Н и дальности полета L определяется начальная скорость тела V и угол α, под которым тело брошено к горизонту. Воспользоваться соотношениями  и
и  .
.
4. Человек, находящийся на краю обрыва высотой Н, бросает с начальной скоростью V камень под углом αк горизонту. Написать программу, которой по введенному пользователем времени t определяется положение камня (высота от дна обрыва x(t) и расстояние до края обрыва y(t)). Предусмотреть случай, когда камень упал на дно обрыва (использовать тернарный оператор). Уравнения движения камня имеют вид: вдоль горизонтальной оси  , вдоль направленной вверх вертикальной оси
, вдоль направленной вверх вертикальной оси  (координата отсчитывается от дна обрыва). Время полета камня Т определяется условием у(Т) = 0, т.е.
(координата отсчитывается от дна обрыва). Время полета камня Т определяется условием у(Т) = 0, т.е.  , откуда получаем
, откуда получаем  .
.
5. Самолет летит на высоте Н над землей со скоростью U. При подлете к наземному объекту он сбрасывает бомбу. Написать программу, которой вычисляется подлетное расстояние S до объекта, на котором производится сбрасывание бомбы. Воспользоваться тем, что бомба до земли летит время  . Расстояние S вычисляется как S = UT.
. Расстояние S вычисляется как S = UT.
6. Лодка плывет из пункта А в пункт Б и обратно. Скорость лодки V, расстояние между пунктами S и скорость течения реки U задаются пользователем. Написать программу, в которой вычисляется общее время движения лодки Т. Учесть, что при движении по течению лодка плывет время  , а при движении против течения на путь между пунктами уходит время
, а при движении против течения на путь между пунктами уходит время 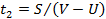 . Общее время
. Общее время  .
.
7. Мотоциклист едет из пункта А в пункт Б и обратно. Написать программу, в которой по известной средней скорости движения V, расстоянию S между пунктами и времени движения t из пункта А в пункт Б вычислить среднюю скорость  мотоциклиста при движении из пункта А в пункт Б и скорость V2 при движении из пункта Б в пункт А. Воспользуйтесь соотношениями
мотоциклиста при движении из пункта А в пункт Б и скорость V2 при движении из пункта Б в пункт А. Воспользуйтесь соотношениями  и
и  .
.
8. Поезд метро едет на протяжении времени t с постоянной скоростью V, а затем такой же промежуток времени тормозит до полной остановки. Написать программу для вычисления пути S, пройденного поездом. При составлении программы воспользуйтесь набором соотношений:  (S1 и S2 пути, пройденные поездом при равномерном и равнозамедленном движении соответственно),
(S1 и S2 пути, пройденные поездом при равномерном и равнозамедленном движении соответственно),  ,
,  , где
, где  - ускорение при равнозамедленном движении. Для сравнения рассчитайте результат по соотношению
- ускорение при равнозамедленном движении. Для сравнения рассчитайте результат по соотношению  .
.
9. Математический маятник совершает колебания по закону  . Частота ωмаятника известна. В начальный момент координата х в k раз меньше амплитуды А. В какой момент времени Т отклонение маятника максимально? Написать программу для определения параметра Т при условии, что параметры ω и k вводятся пользователем. При составлении программы воспользоваться соотношениями
. Частота ωмаятника известна. В начальный момент координата х в k раз меньше амплитуды А. В какой момент времени Т отклонение маятника максимально? Написать программу для определения параметра Т при условии, что параметры ω и k вводятся пользователем. При составлении программы воспользоваться соотношениями  и
и  .
.
10. Написать программу для вычисления ускорения свободного падения gкак функции h высоты над поверхностью Земли на основании значений гравитационной постоянной  , массы Земли
, массы Земли 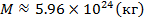 и ее радиуса
и ее радиуса  . Воспользоваться тем, что на тело массой т действует сила
. Воспользоваться тем, что на тело массой т действует сила  , которая по закону всемирного тяготения равна
, которая по закону всемирного тяготения равна  откуда получаем
откуда получаем  .
.
11. Написать программу для вычисления корня квадратного из комплексного числа  . Такая операция на множестве комплексных чисел, как известно, имеет два решения:
. Такая операция на множестве комплексных чисел, как известно, имеет два решения:  и
и 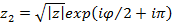 , где
, где  есть модуль комплексного числа z, a φ - его аргумент. Вычислить действительную и мнимую части чисел
есть модуль комплексного числа z, a φ - его аргумент. Вычислить действительную и мнимую части чисел 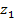 и
и  Параметры х и y вводятся пользователем с клавиатуры.
Параметры х и y вводятся пользователем с клавиатуры.
12. Написать программу для расчета ускорения тела массой т, которое находится на горизонтальной плоскости и к которому под углом α (к горизонту) приложена сила 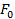 . Коэффициент трения тела о плоскость равен μ. Предусмотреть вариант, когда тело неподвижно (использовать тернарный оператор). Воспользоваться тем, что если тело движется, на него вдоль плоскости движения действует равнодействующая сила
. Коэффициент трения тела о плоскость равен μ. Предусмотреть вариант, когда тело неподвижно (использовать тернарный оператор). Воспользоваться тем, что если тело движется, на него вдоль плоскости движения действует равнодействующая сила  , где сила трения
, где сила трения  . Ускорение тела а ищется из второго закона Ньютона F = та.
. Ускорение тела а ищется из второго закона Ньютона F = та.
13. Тело соскальзывает с наклонной плоскости (угол наклона α) с ускорением а. Написать программу для определения коэффициента трения μ тела о плоскость. Воспользоваться тем, что по второму закону Ньютона  , где сила трения
, где сила трения  . Отсюда получаем
. Отсюда получаем 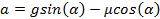 .
.
14. Определить силу трения  , которая действует на тело массой т, находящееся на наклонной плоскости (угол наклона α). Воспользоваться соотношением
, которая действует на тело массой т, находящееся на наклонной плоскости (угол наклона α). Воспользоваться соотношением  для случая, если тело скользит по плоскости, и
для случая, если тело скользит по плоскости, и  если тело находится в покое. Использовать тернарный оператор.
если тело находится в покое. Использовать тернарный оператор.
15. Тело массой т находится на наклонной плоскости (угол наклона α) и привязано с помощью нерастяжимой нити (нить направлена вдоль наклонной плоскости). Коэффициент трения тела о плоскость равен μ. Написать программу, для вычисления силы натяжения нити F. Принять во внимание, что возможны две ситуации. Если  , натяжение нити равно нулю, т.е. F = 0. В противном случае сила натяжения нити
, натяжение нити равно нулю, т.е. F = 0. В противном случае сила натяжения нити  . Использовать тернарный оператор.
. Использовать тернарный оператор.
16. В баллоне под поршнем с идеальным газом находится сыпучее вещество. Написать программу для вычисления объема сыпучего вещества V, если известно, что при объеме под поршнем  давление газа равно
давление газа равно  , а при объеме под поршнем
, а при объеме под поршнем  давление газа равно
давление газа равно 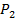 . Использовать соотношение
. Использовать соотношение 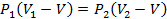 . С помощью тернарного оператора обработать ситуацию, когда числовые значения
. С помощью тернарного оператора обработать ситуацию, когда числовые значения  ,
,  ,
,  и
и 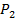 являются некорректными (расчетное значение V < 0).
являются некорректными (расчетное значение V < 0).
17. Написать программу для вычисления работы выхода электрона А, если электрон выбивается фотоном с частотой v, скорость электрона на выходе V. Воспользоваться соотношением
 , где масса электрона
, где масса электрона  , а постоянная Планка
, а постоянная Планка  . Предусмотреть ситуацию, когда введены такие значение v и V, что
. Предусмотреть ситуацию, когда введены такие значение v и V, что  (использовать тернарный оператор).
(использовать тернарный оператор).
18. Написать программу для вычисления кинетической энергии  релятивистского электрона. Использовать формулу
релятивистского электрона. Использовать формулу 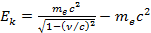 , где масса (масса покоя) электрона
, где масса (масса покоя) электрона  , скорость света
, скорость света  a v - скорость электрона. Для сравнения рассчитайте нерелятивистское выражение
a v - скорость электрона. Для сравнения рассчитайте нерелятивистское выражение  .
.
19. Написать программу для вычисления числа распавшихся ядер Δ N за время t, если в начальный момент ядер было N, а период полураспада равен Т. Использовать формулу  . Предусмотреть в программе возможность вычисления значения Δ N как в абсолютных единицах, так и в процентном отношении к начальному количеству ядер N.
. Предусмотреть в программе возможность вычисления значения Δ N как в абсолютных единицах, так и в процентном отношении к начальному количеству ядер N.
20. Группа из п подводных лодок атакует авианосец. Лодки по очереди выпускают по одной торпеде с ядерным зарядом: если выпущенная лодкой торпеда не попала в авианосец, торпеду выпускает следующая подводная лодка. Вероятность попадания торпеды в авианосец равна р. Выпуская торпеду, лодка демаскирует себя, в силу чего подвергается атаке со стороны кораблей охранения. Вероятность затопления демаскированной подводной лодки кораблями охранения равна  . Написать программу для вычисления вероятности Р(А) события А, состоящего в том, что авианосец будет затоплен, а подводные лодки уйдут из зоны действия кораблей охранения без потерь. Использовать формулу
. Написать программу для вычисления вероятности Р(А) события А, состоящего в том, что авианосец будет затоплен, а подводные лодки уйдут из зоны действия кораблей охранения без потерь. Использовать формулу  где введено обозначение q = (1 — р)(1 — p1).
где введено обозначение q = (1 — р)(1 — p1).
Приложение
 2015-10-22
2015-10-22 2203
2203







