Вращение векторного поля

КУРСОВАЯ РАБОТА

На тему: «Вращение векторного поля. Примеры».

Выполнила: студентка 1 курса магистратуры направления «Педагогическое образование» программа подготовки «Математическое образование»

физико-математического факультета

Шпак И. С.

Научный руководитель:

кандидат физико-математических наук,доцент кафедры высшей математики

Корнев С.В.

Воронеж 2014г.

СОДЕРЖАНИЕ

Введение

1. Вращение векторного поля

1.1. Векторное поле

1.2. Угловая функция

1.3. Вращение поля

1.4. Формула Пуанкаре

1.5. Вычисление вращения

2. Примеры вращения векторного поля

2.1. Дивергенция векторного поля

2.2. Циркуляция

2.3. Ротор и его основные свойства

3. Формулы Грина

4. Формулы Стокса

Заключение

Литература

Введение

Векторный анализ - это раздел векторного исчисления, в котором изучается средствами математического анализа векторные и скалярные функции одного или нескольких аргументов (векторные поля и скалярные поля). Для характеристики данных полей вводится целый ряд понятий, часть которых приведены в данной работе: вращение векторного поля, циркуляция, дивергенция, ротор.

Поле - область пространства, каждой точке которого соответствует определенное значение некоторой физической величины. По своему характеру физические величины могут быть скалярными или векторными. Соответственно поля этих величин также являются скалярными или векторными. Так же в данной работе будут приведены формулы британского математика и физика Джорджа Грина и английского физика-теоретика и математика ирландского происхождения Джорджа Габрие́ля Стокса. Объектом исследования в курсовой работе являются процессы поведения характеристик векторного поля.

Цель написания работы состоит в изучении теории поля с помощью векторного анализа, и закрепить полученные знания по высшей математике.

Вращение векторного поля

1.1. Векторное поле.

Пусть в каждой точке M некоторого плоского множества Ω задан вектор Φ(M), лежащий в той же плоскости. В этом случае будем говорить, что на Ω задано векторное поле Φ. Если на плоскости определена некоторая прямоугольная система координат, то задание векторного поля Φ(M) эквивалентно заданию двух вещественных функций φ(M) и ψ(M) точки M ∈ Ω — компонент векторов Φ(M).

Векторное поле будем называть непрерывным, если функции φ(M), ψ(M) непрерывны.

Векторные поля встречаются и их приходится изучать при решении разнообразных математических задач.

В частности, во многих случаях векторы Φ(M) определяются как сдвиги точек, определяемые некоторым преобразованием A, заданным на Ω:

Φ(M) = A(M) − M.

В качестве второго примера рассмотрим систему дифференциальных уравнений

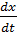= P(x,y), 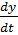= Q(x,y). (1.1)

Если решение этой системы рассматривать как закон движения точки в плоскости с прямоугольными координатами (x,y), то векторное поле

Φ(x,y) = (P(x,y),Q(x,y)) (1.2)

— это поле скоростей движущихся по упомянутым законам точек. Выписать решения системы (1.1) в явном виде обычно невозможно, а общее представление о поле скоростей (1.2) в ряде случаев можно получить без труда. Априори ясно, что общие характеристики поля скоростей должны нести существенную информацию о решениях системы (1.1).

Рассмотрим, наконец, функцию f(z) комплексного переменного z = x + iy. Изучение функции

f(z) = u(x,y) + iv(x,y) (1.3)

равносильно изучению векторного поля

Φ(x,y) = (u(x,y),v(x,y)). (1.4)

1.2. Угловая функция.

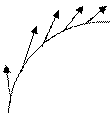
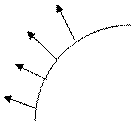
Пусть непрерывное векторное поле Φ(M) задано на некоторой жордановой кривой Γ без самопересечений. Если Γ — гладкая кривая, то примерами могут быть поля единичных касательных или нормальных векторов, направленных в определенную сторону (рис. 1.1).

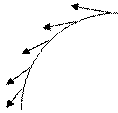Рис. 1.1

Допустим, что кривая Γ задана в параметрической форме:

x = x(t), y = y(t) (a ≤ t ≤ b). (1.5)

Тогда задание векторного поля

Φ(x,y) = (φ(x,y),ψ(x,y)) (1.6)

на кривой Γ равносильно заданию вектор-функции

Φ(t) = (φ(x(t),y(t)),ψ(x(t),y(t))) (1.7)

на отрезке [a,b].

Пусть вектор-функция Φ(t) непрерывна и все векторы Φ(t) не равны нулю. Определим для каждого t ∈ [a,b] угол (в радианах) между векторами Φ(t) и Φ(a), отсчитанный от Φ(a) в положительном направлении (против хода часовой стрелки). Этот угол является многозначной функцией t. Через θ(t) обозначим непрерывную ветвь этой функции, обращающуюся в нуль при t = a, и назовем ее угловой функцией поля Φ на кривой Γ.

В качестве примера рассмотрим векторное поле

Φ(x,y) = (x,y) (1.8)

на кривой (половине единичной окружности)

x = cosπt, y = sinπt (0 ≤ t ≤ 1). (1.9)

Очевидно (рассмотрите чертеж), θ(t) = πt.

Из определения угловой функции вытекает, что она не меняется, если все векторы поля поворачивать на один и тот же угол. Угловая функция не изменится при замене каждого вектора Φ(x,y) единичным вектором того же направления, то есть при переходе к “нормированному” полю

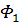(x,y) = 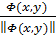(1.10)

(через 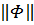здесь и ниже обозначается длина вектора Φ). Формула (1.10) имеет смысл, так как угловая функция определена лишь для полей, не имеющих нулевых векторов.

В заключение пункта подчеркнем, что угловая функция зависит от того, каким способом на кривой Γ введен параметр.

Вращение поля.

Приращение угловой функции θ(t) на всем отрезке [a,b], выраженное в единицах полного оборота, то есть величину

γ(Φ,Γ) = 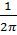(θ(b) − θ(a)) = 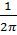θ(b), (1.11)

назовем вращением поля Φ на кривой Γ. Введение на кривой Γ параметра t превращает Γ в ориентированную кривую (перемещение точки при возрастании t задает эту ориентацию — см. рис. 1.2).

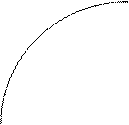Приведенное выше определение вращения векторного поля зависит от способа введения параметра. Нетрудно видеть, что вращение поля Φ на кривой Γ при двух способах введения параметра одинаково, если эти параметры определяют на Γ одинаковую ориентацию. Если же две параметризации определяют разные ориентации, то вращения будут отличаться лишь знаком.

M(b)

Г

M(a)

Рис. 1.2

Таким образом, вращение поля определяется лишь ориентацией кривой.При переходе к противоположной ориентации абсолютная величина вращения сохраняется, а знак вращения меняется.

Из проведенных в предыдущем пункте рассуждений вытекает, что вращение не меняется при повороте всех векторов поля на один и тот же угол и при нормировании поля. Если ориентированная кривая Γ является объединением нескольких ориентированных кривых 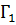, ,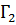..., 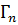(см. рис. 1.3), то вращение поля Φ на Γ равно сумме вращений на , ,..., .

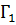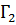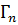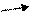
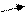
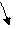
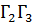
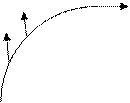
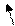
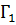
Рис. 1.3

Вращение может быть любым вещественным числом. Чтобы убедиться в этом, достаточно заметить, что θ(t) является угловой функцией поля

Φ(t) = (cosθ(t),sinθ(t)), (1.12)

рассматриваемого на отрезке

x = t, y = 0 (0 ≤ t ≤ 1); (1.13)

вращение γ этого поля равно 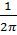θ(1)и может быть любым, так как непрерывная функция θ(t) может выбираться произвольным способом.

Если на двух концах кривой Γ векторы поля Φ направлены одинаково, то изменение угловой функции кратно 2π и, следовательно, вращение является целым числом. Аналогично, если на концах кривой Γ векторы поля Φ направлены противоположно, то γ(Φ,Γ) = n + , где n — некоторое целое число.

Вращение векторного поля параллельных векторов равно нулю, так как в этом случае θ(t) ≡ 0. Однако вращение может быть равно нулю и в других случаях.

Формула Пуанкаре.

Предположим дополнительно, что кривая Γ (x = x(t), y = y(t), a ≤ t ≤ b) кусочно-гладкая, а векторное поле

Φ(x,y) = (φ(x,y),ψ(x,y))

непрерывно дифференцируемо в том смысле, что функции φ(x,y) и ψ(x,y) непрерывно дифференцируемы.

Пустьвектор

Φ(t) = (φ(x(t),y(t)),ψ(x(t),y(t)))

образуетсосьюабсциссугол α(t). Очевидно,

θ(t) = α(t) − α(a)

и

dθ = dα = darctg 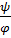= 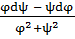. (1.14)

Отсюда вытекает, что

γ(Φ,Γ) = 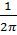(θ(b) − θ(a)) =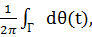

то есть

γ(Φ,Γ) = 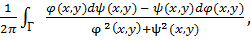(1.15)

Эта формула имеет смысл, так как знаменатель в подынтегральном выражении в нуль не обращается — вращение (как и угловая функция) определено лишь для непрерывных полей без нулевых векторов.

Если положить

φ(x(t),y(t)) = φ(t), ψ(x(t),y(t)) = ψ(t),

то формулу Пуанкаре (1.15) можно записать при помощи обыкновенного интеграла

γ(Φ,Γ) = 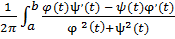dt. (1.16)

Для фактического вычисления вращения формула Пуанкаре малоудобна.

Вычисление вращения.

После введения параметра вычисление вращения поля на произвольной кривой сводится к вычислению вращения поля

Φ(t) = (P(t),Q(t)) (1.17)

на некотором отрезке x = t, y = 0 (a ≤ t ≤ b). При вычислении вращения удобно отрезок [a,b] разбить на части так, чтобы вращение на каждой части вычислялось просто, а затем воспользоваться тем фактом, что вращение на всем отрезке равно сумме вращений на его частях. При вычислении вращения полезно иметь в виду, что вращение равно выраженному в единицах полного оборота наименьшему углу между векторами на концах кривой 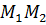, если ни один вектор поля Φ(M) не направлен противоположно вектору Φ(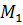) в точке 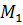(если ни один вектор поля не направлен противоположно вектору Φ(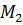) в точке 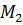). Для доказательства достаточно заметить, что в общем случае вращение отличается от угла между векторами Φ(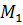) и Φ(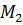) на целое число и что угловая функция поля, вращение которого по абсолютной величине больше ½, принимает либо значение π, либо значение −π (в соответствующей точке вектор поля направлен противоположно Φ(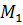)). Допустим, что уравнение

P(t) = 0 (1.18)

имеет на [a,b] конечное число решений

< <... < .

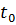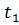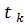Вращение γ поля (1.17) на всем отрезке [a,b] представим как сумму

γ = 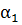+ + 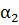+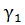... + 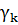, (1.19)

где 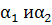— вращения соответственно на отрезках [ 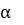, 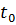] и [ 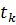,b], а 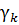— вращение на отрезке [ 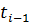, 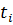] (i = 1,...,k).

На каждом отрезке [ 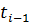, 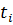] колебание угловой функции θ(t) поля (1.17) не превышает π, так как в противном случае функция P(t) принимала бы нулевое значение в некоторой точке интервала (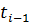, 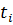). Поэтому каждое 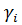принимает одно из трех значений: ½,0,− ½.

Если

sign Q( 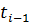) = sign Q( ),

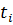то векторы поля на концах отрезка [ 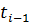, 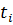] направлены одинаково и поэтому 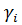= 0.

Пусть

sign Q( 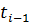) = 1, sign Q( 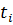) = −1.

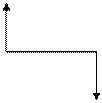
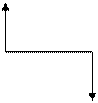
Тогда (см. рис. 1.4) 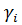= −½при P (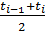) > 0 и 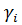= ½при P(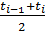) < 0.

Аналогично при

sign Q( 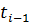) = −1, sign Q( 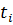) = 1

вращение γi вычисляется по правилу 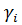= −½при P (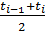) < 0 и 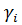= ½при P(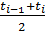) >0.

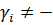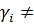½ ½

P(t)>0 P(t)<0

Рис. 1.4

Все перечисленные случаи можно охватить общей формулой

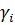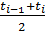= signP()(signQ(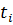) − signQ(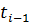)), (1.20)

проверкукоторойпредоставляемчитателю. Формула (1.19) перепишетсятогдаввиде

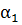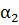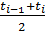γ = + + signP()(signQ(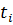) − signQ(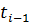)). (1.21)

При применении этой формулы полезно помнить, что P(t) на интервале (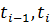) принимает значения одного знака. В качестве примера рассмотрим поле

Φ (x,y) = (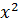 − 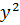,10 xy)

на той половине единичной окружности, которая выделена неравенством y ≥ 0, с параметром t = x. Функции P(t) и Q (t) определяются равенствами

P(t) = 2 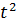− 1, Q(t) = 10t 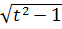(−1 ≤ t ≤ 1).

Уравнение P(t) = 0 имеет два корня: 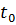= − 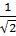, 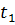= 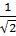. Направление векторов Φ(−1) и Φ(1) совпадает с положительным направлением оси абсцисс. Векторы Φ(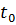) и Φ(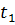) направлены соответственно по отрицательному и положительному направлению оси ординат. Поэтому 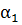= = 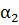− . Из формулы (1.21) вытекает, что вращение рассматриваемого поля равно −1.

Нетрудно видеть, что формула (1.21) сохраняет силу, если сумму в ней брать только по таким парам соседних нулей функции P(t), между которыми есть нули функции Q(t). В этой последней форме формула (1.21) верна и в том случае, когда уравнение P(t) = 0 имеет бесконечное множество нулей.

Некоторые свойства вращения.

1. При изменении ориентации линии L на противоположную значение g(L; А) умножается на -1.

2. Если линия L разбита на несколько частей, ориентированных в соответствии с ориентацией L, то вращение поля вдоль L равно сумме его вращений вдоль всех частей.

3. Если линия L замкнутая, то g(L; А) - целое число, не зависящее от того, какая точка на L была принята за начальную.

4. Если замкнутая линия L непрерывно деформируется так, что в любой момент процесса деформации она не проходит через особые точки поля, то вращение поля вдоль деформируемой линии остается неизменным.

5. Если на замкнутой линии L и внутри нее нет особых точек поля А, то g(L; А) = 0.