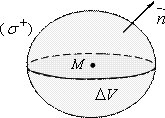
Дивергенция (или расходимость) векторного поля 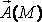 в точке М - это предел отношения потока вектора
в точке М - это предел отношения потока вектора 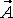 через замкнутую поверхность
через замкнутую поверхность 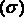 окружающую точку М, в направлении ее внешней нормали к объему, ограниченному этой поверхностью, при условии, что вся поверхность
окружающую точку М, в направлении ее внешней нормали к объему, ограниченному этой поверхностью, при условии, что вся поверхность 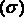 , стягивается в точку М:
, стягивается в точку М:
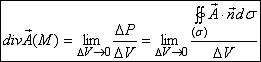 (1)
(1)
Основные свойства дивергенции:
1. 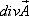 - это дифференциальная характеристика поля, является скалярной величиной.
- это дифференциальная характеристика поля, является скалярной величиной.
2.В каждой точке М поля 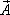 показывает наличие источников или стоков поля:
показывает наличие источников или стоков поля:
3. если 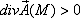 , то в точке М есть источник поля
, то в точке М есть источник поля 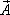 , при этом значение
, при этом значение 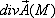 численно равно мощности источника;
численно равно мощности источника;
4. если 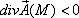 , то в точке М есть сток поля
, то в точке М есть сток поля 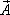 при этом значение
при этом значение 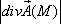 численно равно мощности стока;
численно равно мощности стока;
5. если 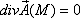 , то в точке М нет ни источника, ни стока поля
, то в точке М нет ни источника, ни стока поля 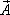
6. 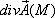 вычисляется по формуле:
вычисляется по формуле:
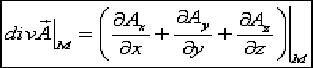
Воспользуемся формулой Остроградского-Гаусса, связывающей интеграл по замкнутой поверхности с интегралом по объёму, ограниченному этой поверхностью:
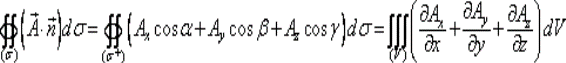
Применяем теорему о среднем к тройному интегралу:
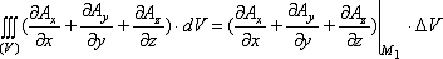
где 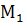 - это некоторая фиксированная точка в объёме, ограниченном замкнутой поверхностью (σ),
- это некоторая фиксированная точка в объёме, ограниченном замкнутой поверхностью (σ),
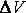 -величина этого объёма.
-величина этого объёма.
Теперь используем определение (1) дивергенции:
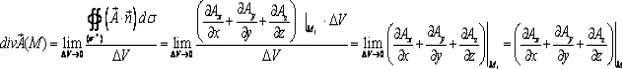
Так как при 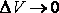 точка
точка 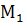 стремится к точке M.
стремится к точке M.
Если использовать понятие дивергенции, то теорема Остроградского-Гаусса в векторной форме:
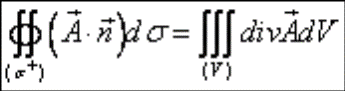
то есть поток вектора 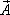 изнутри замкнутой поверхности
изнутри замкнутой поверхности 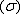 равен тройному интегралу от дивергенции вектора
равен тройному интегралу от дивергенции вектора 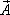 по объему, ограниченному этой поверхностью.
по объему, ограниченному этой поверхностью.
Так как 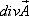 можно рассматривать как плотность распределения источников и стоков векторного поля
можно рассматривать как плотность распределения источников и стоков векторного поля 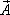 то тройной интеграл
то тройной интеграл
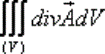
равен суммарной мощности источников и стоков по объему 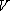 .
.
Учитывая это, смысл теоремы Остроградского-Гаусса в форме (3) можно сформулировать следующим образом: поток векторного поля 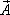 изнутри замкнутой поверхности
изнутри замкнутой поверхности 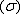 равен суммарной мощности источников и стоков этого поля, заключенных в объеме
равен суммарной мощности источников и стоков этого поля, заключенных в объеме 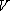 , ограниченном этой поверхностью
, ограниченном этой поверхностью 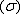 .
.
Следовательно, если поток равен 0, то внутри поверхности 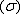 нет источников и стоков поля
нет источников и стоков поля 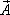 или они уравновешивают друг друга.
или они уравновешивают друг друга.
Линейность дивергенции:
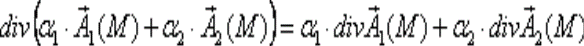
Это следует из линейности операций сложения векторов и дифференцирования.
Дивергенция произведения скалярного поля 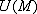 на векторное поле
на векторное поле 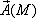 вычисляется по формуле:
вычисляется по формуле:
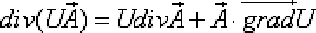
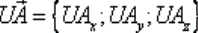
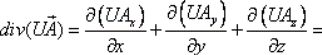
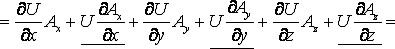
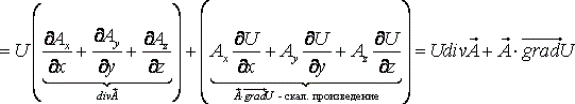
Примеры 1 (вычисление дивергенции векторного поля)
Дано 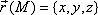 - поле радиус-вектора точки
- поле радиус-вектора точки 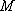 . Вычислить
. Вычислить 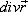
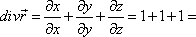 Решение
Решение  3
3
то есть каждая точка М этого поля является источником постоянной мощности, равной 3.
Вычислить 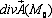 и объяснить смысл ее значения, если
и объяснить смысл ее значения, если
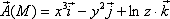
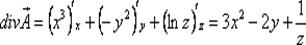 Решение
Решение
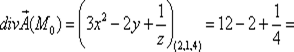 |
10,25
Значение 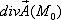 указывает на то, что в заданной точке
указывает на то, что в заданной точке 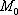 есть источник векторного поля
есть источник векторного поля 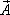 и мощность этого источника равна 10,25.
и мощность этого источника равна 10,25.
По рассмотренному примеру можно заметить, что любое векторное поле 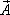 сопровождается скалярным полем
сопровождается скалярным полем 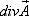 его дивергенций.
его дивергенций.
Циркуляция
Циркуля́цией ве́кторного по́ля называется криволинейный интеграл второго рода, взятый по произвольному замкнутому контуру Γ. По определению.
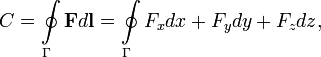
Где 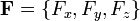 - векторное поле (или вектор-функция), определенное в некоторой области D, содержащей в себе контур Γ,
- векторное поле (или вектор-функция), определенное в некоторой области D, содержащей в себе контур Γ, 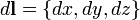 - бесконечно малое приращение радиус-вектора
- бесконечно малое приращение радиус-вектора 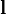 вдоль контура. Окружность на символе интеграла подчёркивает тот факт, что интегрирование производится по замкнутому контуру. Приведенное выше определение справедливо для трёхмерного случая, но оно, как и основные свойства, перечисленные ниже, прямо обобщается на произвольную размерность пространства.
вдоль контура. Окружность на символе интеграла подчёркивает тот факт, что интегрирование производится по замкнутому контуру. Приведенное выше определение справедливо для трёхмерного случая, но оно, как и основные свойства, перечисленные ниже, прямо обобщается на произвольную размерность пространства.
Аддитивность:
Циркуляция по контуру, ограничивающему несколько смежных поверхностей, равна сумме циркуляций по контурам, ограничивающим каждую поверхность в отдельности, то есть
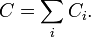
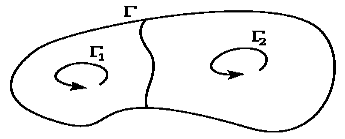
Свойство аддитивности циркуляции: циркуляция по контуру Γ есть сумма циркуляций по контурам 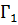 и
и 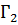 , то есть C =
, то есть C =  +
+ 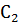
Формула Стокса:
Циркуляция вектора F по произвольному контуру Г равна потоку вектора 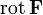 через произвольную поверхность S, ограниченную данным контуром.
через произвольную поверхность S, ограниченную данным контуром.
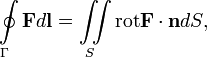
Где
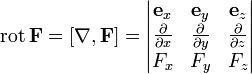
Ротор вектора F.
В случае, если контур плоский, например лежит в плоскости OXY, справедлива теорема Грина
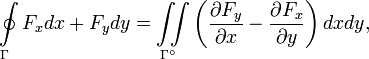
Где 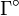 - плоскость, ограничиваемая контуром Γ (внутренность контур).
- плоскость, ограничиваемая контуром Γ (внутренность контур).
 2015-10-22
2015-10-22 22678
22678








