Свойства матричных операций

Умножение матриц

Определение

Пусть даны две прямоугольные матрицы и размерности и соответственно:

Тогда матрица размерностью называется их произведением:

где:

Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором; в этом случае говорят, что форма матриц согласована. В частности, умножение всегда выполнимо, если оба сомножителя — квадратные матрицы одного и того же порядка.

Следует заметить, что из существования произведения вовсе не следует существование произведения

Иллюстрация

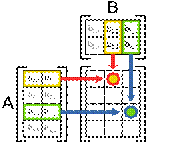
Произведение матриц AB состоит из всех возможных комбинаций скалярных произведений вектор-строк матрицы A и вектор-столбцов матрицы B. Элемент матрицы AB с индексами i, j есть скалярное произведение i -ой вектор-строки матрицы A и j -го вектор-столбца матрицы B.

Иллюстрация справа демонстрирует вычисление произведения двух матриц A и B, она показывает как каждые пересечения в произведении матриц соответствуют строкам матрицы A и столбцам матрицы B. Размер результирующей матрицы всегда максимально возможный, то есть для каждой строки матрицы A и столбца матрицы B есть всегда соответствующее пересечение в произведении матрицы.

Значения на пересечениях отмеченных кружочками будут:

В общем случае, произведение матриц не является коммутативной операцией. К примеру:

Элемент произведения матриц, приведённых выше, вычисляется следующим образом

Первая координата в обозначении матрицы обозначает строку, вторая координата — столбец; этот порядок используют как при индексации, так и при обозначении размера. Элемент на пересечении строки и столбца 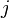результирующей матрицы является скалярным произведением -й строки первой матрицы и 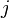-го столбца второй матрицы. Это объясняет почему ширина и высота умножаемых матриц должны совпадать: в противном случае скалярное произведение не определено.

Элементарными преобразованиями матрицы называют следующие операции:

 перестановка любых двух строк матрицы;

 умножение любой строки на произвольное, отличное от нуля, число;

 сложение любой строки с другой строкой, умноженной на произвольное число;

 транспонирование матрицы.

Матрица A ^T называется транспонированной по отношению к матрице A = { a_ij }, если A^T= {a _ji }:

Иными словами, матрица, получающаяся из матрицы A заменой строк столбцами, называется транспонированной по отношению к матрице A и обозначается A ^T.

Элементарные преобразования не меняют ранга матрицы.

Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц, то есть, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.

Определение.

Матрица называется обратной для матрицы , определитель которой отличен от нуля , если справедливы равенства , где E – единичная матрица порядка n на n.

матрицы, минора матрицы и алгебраического дополнения элемента матрицы.

Определение.

Минор k-ого порядка матрицы A порядка m на n – это определитель матрицы порядка k на k, которая получается из элементов матрицы А, находящихся в выбранных k строках и k столбцах. (k не превосходит наименьшего из чисел m или n).

Минор (n-1)-ого порядка, который составляется из элементов всех строк, кроме i-ой, и всех столбцов, кроме j-ого, квадратной матрицы А порядка n на n обозначим как .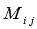

Иными словами, минор 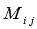получается из квадратной матрицы А порядка n на n вычеркиванием элементов i-ой строки и j-ого столбца.

Для примера запишем, минор 2-ого порядка, который получаетсся из матрицы 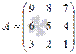выбором элементов ее второй, третьей строк и первого, третьего столбцов . Также покажем минор, который получается из матрицы вычеркиванием второй строки и третьего столбца . Проиллюстрируем построение этих миноров: и .

Определение.

Алгебраическим дополнением элемента квадратной матрицы называют минор (n-1)-ого порядка, который получается из матрицы А, вычеркиванием элементов ее i-ой строки и j-ого столбца, умноженный на .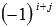

Алгебраическое дополнение элемента обозначается как . Таким обрзом, .

Например, для матрицы алгебраическое дополнение элемента есть .

Во-вторых, нам пригодятся два свойства определителя, которые мы разобрали в разделе вычисление определителя матрицы:

·

·

На основании этих свойств определителя, определения операции умножения матрицы на число и понятия обратной матрицы справедливо равенство , где - транспонированная матрица, элементами которой являются алгебраические дополнения .

Матрица действительно является обратной для матрицы А, так как выполняются равенства . Покажем это

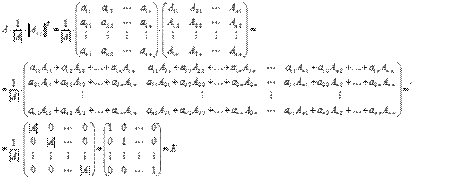
Составим алгоритм нахождения обратной матрицы с использованием равенства .

1. Вычисляем определитель матрицы А и убеждаемся, что он отличен от нуля (в противном случае матрица А необратима).

2. Строим 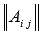- матрицу из алгебраических дополнений элементов .

3. Транспонируем матрицу 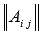, тем самым получаем .

4. Умножаем каждый элемент матрицы на число . Этой операцией завершается нахождение обратной матрицы .

5. Проводим проверку результата, вычисляя произведения и . Если , то обратная матрица найдена верно, в противном случае где-то была допущена ошибка.