2015-10-22
356
Это знаменитая формула Муавра.
Здесь k - целое. Чтобы получить n различных значений корня n -ой степени из z необходимо задать n последовательных значений для k (например, k = 0, 1, 2,…, n – 1).
Геометрическое представление комплексных чисел. Действительные числа изображаются точками на числовой прямой:
Здесь точка A означает число –3, точка B – число 2, и O – ноль. В отличие от этого комплексные числа изображаются точками на координатной плоскости. Выберем для этого прямоугольные (декартовы) координаты с одинаковыми масштабами на обеих осях. Тогда комплексное число a+ bi будет представлено точкой Р с абсциссой а и ординатой b (см. рис.). Эта система координат называется комплексной плоскостью.
Модулем комплексного числа называется длина вектора OP, изображающего комплексное число на координатной (комплексной) плоскости. Модуль комплексного числа a+ bi обозначается | a+ bi | или буквой r и равен:
Сопряжённые комплексные числа имеют одинаковый модуль.
Аргумент комплексного числа - это угол 
между осью OX и вектором OP, изображающим это комплексное число. Отсюда, tan = b / a.
|
|
|
Первообразный корень по модулю m ― целое число g такое, что 
и 
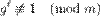при 
где 
― функция Эйлера. Другими словами, первообразный корень — это образующий элемент мультипликативной группы кольца вычетов по модулю m
Свойства
Существование
Первообразные корни существуют только по модулям 
вида
,
где 
― простое число. Только в этих случаях мультипликативная группа кольца вычетов по модулю m является циклической группой порядка .
