ЛЕКЦИЯ № 8
1.23.Достаточные признаки сходимости Признак Даламбера
Признак Даламбера не требует для установления сходимости или расходимости числовых рядов с положительными членами привлечения других, известных рядов для сравнения. Для анализа сходимости числового ряда нужно производить некоторые операции над самим рядом.
Теорема 1 .(Признак Даламбера). Если для числового ряда с положительными членами  существует конечный или бесконечный придел
существует конечный или бесконечный придел  , то ряд сходится при
, то ряд сходится при  и расходится при
и расходится при  . В случае
. В случае 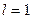 признак не способен различить сходящийся или расходящийся числовой ряд.
признак не способен различить сходящийся или расходящийся числовой ряд.
Доказательство. По определению предела  для любого
для любого  найдется натуральное число
найдется натуральное число  такое, что при
такое, что при  выполняется неравенство
выполняется неравенство  или
или 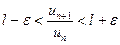 .
.
Рассмотрим случай  . Можно подобрать
. Можно подобрать 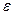 так, что число
так, что число  . Обозначим
. Обозначим  ,
,  . Тогда из правой части неравенства
. Тогда из правой части неравенства 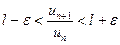 получаем
получаем  , или
, или  при
при  >
>  . Считая, что
. Считая, что  , и придавая номеру
, и придавая номеру  различные значения, получим серию неравенств:
различные значения, получим серию неравенств:

т.е. члены ряда  меньше соответствующих членов ряда
меньше соответствующих членов ряда

который сходится как ряд геометрической прогрессии со знаменателем 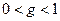 . Но тогда на основании признака сравнения сходится ряд
. Но тогда на основании признака сравнения сходится ряд  , являющийся остатком исходного числового ряда. Следовательно, на основании первой теоремы о свойствах числовых рядов сходится и исходный ряд.
, являющийся остатком исходного числового ряда. Следовательно, на основании первой теоремы о свойствах числовых рядов сходится и исходный ряд.
Рассмотрим случай  . В этом случае
. В этом случае  , поэтому, начиная с некоторого номера
, поэтому, начиная с некоторого номера  , выполняется неравенство
, выполняется неравенство  , или
, или  , т.е. члены ряда возрастают с увеличением номера
, т.е. члены ряда возрастают с увеличением номера  . Поэтому
. Поэтому  . Поскольку не выполняется необходимое условие сходимости, то числовой ряд обязательно расходится.
. Поскольку не выполняется необходимое условие сходимости, то числовой ряд обязательно расходится.
Признак Даламбера целесообразно применять, когда общий член ряда как функция целочисленного аргумента содержит выражение вида  или
или  , т.е. убывает быстрее степенной функции.
, т.е. убывает быстрее степенной функции.
Пример 16. Исследовать на сходимости ряд 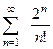 .
.
Решение: Находим
 .
.
Так как  , то данный ряд по признаку Даламбера сходится.
, то данный ряд по признаку Даламбера сходится.
Пример 17. Исследовать на сходимость ряда 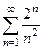 .
.
Решение: Вычисляем

 .
.
Так как  , то данный ряд по признаку Даламбера расходится.
, то данный ряд по признаку Даламбера расходится.
Пример 18. Исследовать сходимость ряда  .
.
Решение. Применим признак Даламбера. Имеем 
 , значит,
, значит, 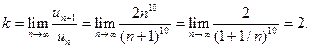 Так как
Так как  , то ряд расходится.
, то ряд расходится.
Пример 19. Исследовать сходимость ряда 
Решение. Применим признак Даламбера. Имеем 
 , поэтому
, поэтому  Следовательно, ряд сходится.
Следовательно, ряд сходится.
Радикальный признак Коши
Если в формуле общего члена числового ряда с положительными членами содержится  -ная степень какого-либо выражения, то удобно пользоваться радикальным признаком Коши.
-ная степень какого-либо выражения, то удобно пользоваться радикальным признаком Коши.
Теорема (Радикальный признак Коши). Если для числового ряда с положительными членами  существует конечный или бесконечный придел
существует конечный или бесконечный придел  , то ряд сходится при
, то ряд сходится при  и расходится при
и расходится при  . В случае
. В случае 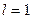 вопрос о сходимости ряда остается открытым.
вопрос о сходимости ряда остается открытым.
Доказательство.
По определению предела последовательности:
 ,
, 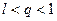 ;
;  . Следовательно,
. Следовательно,

 , или
, или  для
для  .Таким образом, имеем
.Таким образом, имеем
Т.к. члены ряда (1) меньше, чем члены ряда (2), в который входит прогрессия, следовательно ряд (2) сходящийся.
Пример 20. Исследовать на сходимость ряд  .
.
Решение: Применим радикальный признак Коши к ряду  .Вычислим
.Вычислим  .
.
По радикальному признаку Коши исходный ряд сходится.
Пример 21. Исследовать сходимость ряда 
Решение. Применим признак Коши. Здесь  .
.
Поскольку,  ,
,
 , то вычисляем
, то вычисляем  Так как
Так как  , то ряд сходится.
, то ряд сходится.
Пример 22. Исследовать сходимость ряда 
Решение. Применим признак Коши. Здесь  . Поскольку,
. Поскольку, 
 , то вычисляем
, то вычисляем

Так как  , то ряд расходится.
, то ряд расходится.
 2015-10-22
2015-10-22 7776
7776







