Знакочередующиеся ряды. Признак Лейбница

Знакочередующимся рядом называется ряд вида , где для всех . Для знакочередующихся рядов имеет место достаточный признак сходимости, называемый признаком Лейбница.

- знакочередующийся - знакопеременный

Теорема. Знакочередующийся ряд сходится, если члены знакочередующегося ряда монотонно убывают по абсолютной величине, т.е. , а предел модуля общего члена ряда стремится к нулю: .

Доказательство. Рассмотрим частичную сумму четного числа членов ряда . Имеем

Выражение в каждой скобке, согласно первому условию теоремы, положительно, поэтому сумма возрастает с возрастанием номера . Частичную сумму можно записать по-другому:

Очевидно, что . Поскольку последовательность 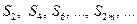возрастает и ограничена с верху, то она имеет предел , причем .

Рассмотрим теперь частичные суммы нечетного числа членов ряда . Так как , то

где было использовано, что .

Так как как при четном , так и при нечетном , то знакочередующийся ряд сходится, причем .

Ряды, для которых выполняются условия теоремы Лейбница, называются лейбницевскими.

Соотношение имеет широкое применение, так как позволяет получить удобную оценку ошибки, которую мы допускаем, заменяя сумму знакочередующегося ряда частичной суммой . -ный остаток знакочередующегося ряда представляет собой также знакочередующийся ряд, сумма которого по модулю меньше первого члена этого ряда, т.е. . Поэтому ошибка должна быть меньше модуля первого из отброшенных членов.

Пример 1. Вычислить приближённо сумму ряда .

Решение: Данный ряд является сходящимся, поскольку выполняются все условия признака Лейбница. Для приближенного вычисления суммы ряда ограничимся шестью первыми членами ряда: