2015-10-22
1910
Задача 1. Представить вектор x в виде линейной комбинации векторов a1, a2, a3, если система векторов a1, a2, a3 линейно независима. В случае линейной зависимости векторов a1, a2, a3 заменить один из них на вектор x так, чтобы полученная система стала линейно независимой.
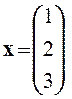
Вариант 1 Вариант 2
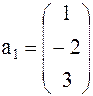
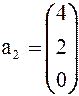
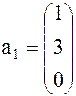
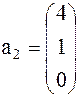
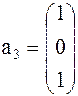
Вариант 3 Вариант 4
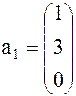
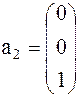
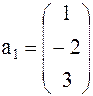
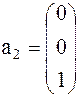
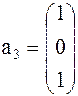
Вариант 5 Вариант 6
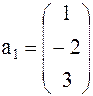
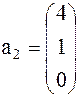
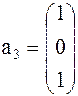
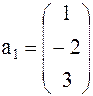
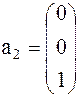
Вариант 7 Вариант 8
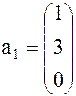
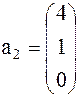
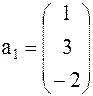
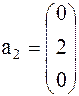
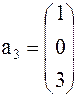
Вариант 9 Вариант 10
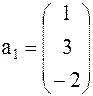
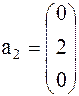
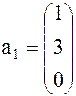
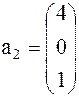
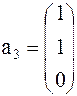
Задача 2. Найти матрицу линейного преобразования, переводящего каждый вектор x двухмерного линейного пространства в вектор y по следующему алгоритму:
| Вариант 1. | Симметричное отображение относительно прямой x1 = 0, а затем поворот на 90° по часовой стрелке. |
| Вариант 2. | Симметричное отображение относительно прямой x2 = 0, а затем поворот на 90° против часовой стрелки. |
| Вариант 3. | Симметричное отображение относительно прямой x1 = 0, а затем симметричное отображение относительно прямой x2 = 0. |
| Вариант 4. | Симметричное отображение относительно прямой x2 = 0, а затем симметричное отображение относительно прямой x1 = 0. |
| Вариант 5. | Симметричное отображение относительно начала координат, а затем поворот на 90° против часовой стрелки. |
| Вариант 6. | Симметричное отображение относительно прямой x2 = 0, а затем симметричное отображение относительно начала координат. |
| Вариант 7. | Симметричное отображение относительно начала координат, а затем симметричное отображение относительно прямой x1 = 0. |
| Вариант 8. | Симметричное отображение относительно начала координат, а затем симметричное отображение относительно прямой x2 = 0. |
| Вариант 9. | Поворот по часовой стрелке на 90°, а затем симметричное отображение относительно прямой x2 = 0. |
| Вариант 10. | Симметричное отображение относительно прямой x1 = 0, а затем поворот на 90° против часовой стрелки. |
Задача 3. Найти собственные значения и собственные векторы линейного оператора, заданного матрицей
Вариант 1 Вариант 2 Вариант 3
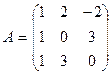
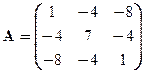
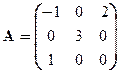
Вариант 4 Вариант 5 Вариант 6
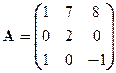
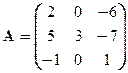
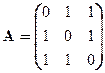
Вариант 7 Вариант 8 Вариант 9
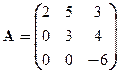
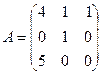
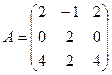
Вариант 10
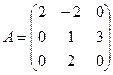
Задача 4. Данную квадратичную форму записать в матричном виде, привести к каноническому виду и выписать матрицу соответствующего линейного преобразования.
Вариант 1.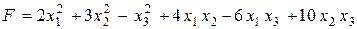 
.
Вариант 2.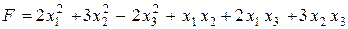 
.
Вариант 3.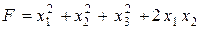 
.
Вариант 4.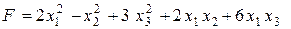 
.
Вариант 5.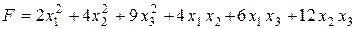 
.
Вариант 6.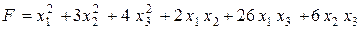 
.
Вариант 7.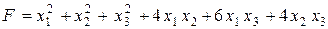 
.
Вариант 8.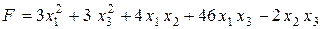 
.
Вариант 9. 
.
Вариант 10.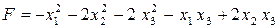 
.
Задача 5. Даны вершины треугольника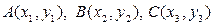 
. Составить: а) уравнения медианы и высоты треугольника 
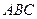, проведенные из вершины 
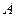; б) уравнение биссектрисы внутреннего угла 
.
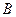| A | B | C | |
| Вариант 1 | (3,1) | (-13,-11) | (-6,-3) |
| Вариант 2 | (26,-5) | (2,2) | (-2,-1) |
| Вариант 3 | (-2,3) | (-18,-9) | (-11,15) |
| Вариант 4 | (6,8) | (-1,-2) | (1,-7) |
| Вариант 5 | (5,4) | (3,-9) | (-12,8) |
| Вариант 6 | (14,-2) | (11,8) | (15,-6) |
| Вариант 7 | (-21,4) | (4,10) | (-6,7) |
| Вариант 8 | (-3,-4) | (8,-7) | (16,12) |
| Вариант 9 | (22,8) | (4,14) | (-5,9) |
| Вариант 10 | (-8,-7) | (6,16) | (-4,-14) |
Задача 6. Найти уравнение нормали, проходящей через начало координат, к плоскости Ax+By+Cz+D=0. Найти координаты точки пересечения плоскости и нормали. Записать уравнение плоскости в виде уравнения плоскости, проходящей через эту точку.
| A | B | C | D | |
| Вариант 1 | -1 | |||
| Вариант 2 | -1 | |||
| Вариант 3 | -2 | -4 | ||
| Вариант 4 | -2 | -1 | -4 | |
| Вариант 5 | -2 | -1 | -2 | |
| Вариант 6 | -1 | |||
| Вариант 7 | -1 | -3 | ||
| Вариант 8 | -2 | |||
| Вариант 9 | -1 | |||
| Вариант 10 | -1 | -3 | -3 |
