1. Можно доказать утверждение, что если в пространстве задана прямоугольная система координат ОХУZ, то всякое уравнение первой степени с тремя неизвестными х,у,z необходимо и достаточно определяет относительно этой системы некоторую плоскость Р. Уравнение это называется общим уравнением плоскости и имеет следующий вид:
А х + В у + С z + D= 0 (17)
(сравните с общим уравнением (15) прямой на плоскости, которое следует из этого при z = 0) и определяет плоскость Р, перпендикулярную вектору 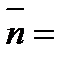 (А,В,С).
(А,В,С).
Вектор  - нормальный вектор плоскости Р.
- нормальный вектор плоскости Р.
Уравнению (17) эквивалентны следующие уравнения.
2. Уравнение плоскости, проходящей через заданную точку М(х0, у0, z0):
А(х - х 0) + В(у - у 0) + С(z - z 0) = 0.
3. Уравнение плоскости в отрезках
 ,
,
где 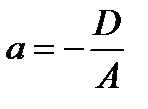 ;
;  ;
;  .
.
4. Уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой, записывается в виде определителя
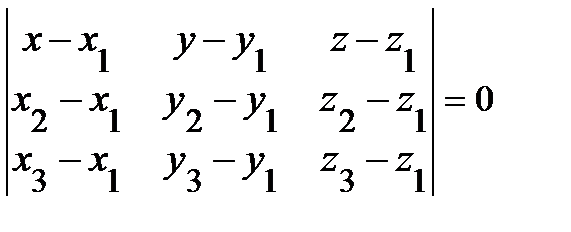 ,
,
где (х 1, y 1, z 1), (х 2, y 2, z 2), (х 3, y 3, z 3) - координаты заданных точек.
Угол между двумя плоскостями определяется как угол между их нормальными векторами n 1 и n 2. Отсюда условие параллельности плоскостей
Р 1 и Р 2:

и условие перпендикулярности двух плоскостей:
А 1 А 2 + В 1 В 2 + С 1 С 2 = 0.
Пример 29. Через точку К (1, -3, 2) провести плоскость, параллельную векторам
а = (1, 2, -3) и b = (2,-1,-1).
Решение. Пусть М (х, у, z) – произвольная точка искомой плоскости. Вектор
КМ = (х - 1, у + 3, z - 2) лежит в этой плоскости, а векторы а и b ей параллельны. Следовательно, векторы КМ, а и b – компланарны. Тогда их смешанное произведение равно нулю:
 .
.
Отсюда -(х –1) - (у + 3) – 5(z – 2) = 0 или х+ 7 у + 5 z + 10 = 0. Это и есть искомое уравнение плоскости.
Различные виды уравнения прямой в пространстве
Прямую линию в пространстве можно задавать в виде:
1) линии пересечения двух не совпадающих и не параллельных плоскостей Р 1 и Р 2:
 ;
;
2) уравнения прямой, проходящей через данную точку М (х 0, у 0, z 0) в направлении, задаваемом вектором L = (m, n, p):
 ,
,
которое называется каноническим уравнением прямой в пространстве;
3) уравнения прямой, проходящей через две заданные точки М (х 1, у 1, z 1)
и M (x 2, y 2, z 2):
 ;
;
4) параметрических уравнений:
 .
.
Пример 30. Привести к каноническому и параметрическому видам уравнение прямой
 .
.
Решение. Прямая задана как линия пересечения двух плоскостей. Нормальные векторы этих плоскостей n 1 = (3,1,-2) и n 2 = (4,-7,-1) перпендикулярны к искомой прямой, поэтому их векторное произведение [ n 1, n 2] = L параллельно ей и вектор [ n 1, n 2] (или любой ему коллинеарный) можно принять за направляющий вектор L искомой прямой.
Находим
[ n 1, n 2] =  .
.
Примем за L = 3 i + j + 5 k. Остается найти какую-либо точку на заданной прямой. Положим для этого, например, z = 0. Получим
 .
.
Решив эту систему, находим х = 1, у = - 2. Таким образом, точка К (1, -2, 0) принадлежит заданной прямой, а её каноническое уравнение имеет вид
 .
.
Параметрические уравнения следуют из канонических, если за параметр t принять каждое из отношений:
 ;
;  ;
;  .
.
Откуда  .
.
Пример 31. Через точку К (1, 3, -1) провести прямую, перпендикулярную
плоскости 3 х – у + 2 z – 10 = 0.
Решение. Вектор нормали к данной плоскости n = (3, -1, 2). Искомая прямая проходит через точку К и должна быть параллельна вектору n. Поэтому её уравнение можно записать в виде
 .
.
1. Объясните смысл параметров в уравнениях
 ;
;  .
.
2. Напишите уравнения:
а) плоскости ХОZ;
б) осей ОУ, ОХ, ОZ.
3. Каково взаимное расположение прямой
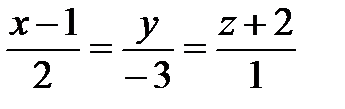
и плоскости 3 х + 2 у – 5 = 0?
 2017-10-25
2017-10-25 9133
9133
