2015-10-22
368
Пр-ная ф-ция наз-ся неоклассической мультипликативной ф-цией, если она непрерывна и удет усл-ям:
1) F (0 ,L) = F(K,0) =0 - отсутствие одного из ресурсов не обеспечивает результата (продукта) производства;
2) 
- с ростом объемов ресурсов растет и объем
выпускаемого продукта;
3) 
- с ростом объемов ресурсов скорость роста
объема продукта снижается;
4) 
- с неограниченным ростом объема одного из ресурсов выпуск продукта неограниченно растет.
Мультипликативная пр-ная ф-ция явл. степ. ф-цей и задается следующим аналит. выр-ем:
где А - коэффициент технического прогресса; α, β- пок-ли степени пр-ной ф-ции соответственно при ср-вах пр-ва и рабочей силе. Как отмечалось, в частном случае, когда 
мультипликатив. пр-ная ф-ция называется функцией Кобба - Дугласа.
18. Изокванты и изоклины мультипликатив. производств.ф-ции. Изоквантой, или линией уровня на плоскости KOL, наз-ся мн-во точек пл-ти, для кот. F(K,L) – Y0 = const. Для мультипликативной пр-ной ф-ции изокванта имеет вид:
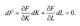Она предст. степенную гиперболу, асимптотами которой являются оси координат ОК и OL. Для разных значений К и L, кот. формируют точку на конкретной изокванте, объем производимого продукта равняется значению Y0. Так как на изокванте справедливо равенство 
, то диф-ал пр-ной ф-ции
|
|
|
Изоклинами наз-ся линии на плоскости KOL наиболее быстрого роста пр-ной ф-ции. Изоклины ортогональны линиям нулевого роста, т.е. ортогональны изоквантам. Поскольку направления наиболее быстрого роста в каждой точке (K, L) задается градиентом
, то уравнение изоклины можно записать
следующим образом:
