Структура множества действительных чисел.
1) N – мн-во натуральных чисел {1, 2, …, n} (сложение, умножение)
2) Z – мн-во целых чисел {0, ±1, ±2, …, ±n, …} (сложение, умножение, вычитание)
3) Q - мн-во рациональных чисел {m/n, mЄZ, nЄN}
Иррациональные числа представимы в виде бесконечной непериодической дроби.
4) R - мн-во действительных чисел. Рациональные и иррациональные числа вместе.
Свойства множества действительных чисел.
1. R – упорядоченное множество.для любых двух различных вещественных чисел a и b выполняется либо a<b, либо a>b.
2. R – плотное мн-во. Между любыми двумя различными числами a и b существует бесконечное мн-во действительных чисел.
3. R – непрерывное мн-во. Св-во непрерывности позволяет установить соответствие между эл-ми мн-ва R и точками оси, т.е. каждой точке действительной оси соответствует вполне определенное действительное число и наоборот.
Опред. Мн-во действительных чисел R будем называть расширенной системой действит. чисел, если к нему присоединены два несобственных числа +∞ и - ∞, удовлетворяющие след. условию: если х – конечное, то
1) х +∞=+∞
2) х -∞=-∞
3) х/± ∞=0
4) ± ∞/x= ±∞, если x>0
∓∞, если x<0
5) x*(±∞)= ±∞, если x>0
∓∞, если x<0
2. Числовые подмножества.
Опред. Пусть А и В-два мн-ва. Если каждый эл-нт мн-ва А является эл-том мн-ва В, то мн-во А называется подмн-вом мн-ва В.
Числовые промежутки.(E c R).
1) Е = [a, b] = {xЄR, a≤x≤b} – отрезок(закрытый промежуток)
2) Е = (a, b) = {xЄR, a<x,b} – интервал(открытый промежуток)
3) E = [a, b) = {xЄR, a≤x<b} – полуинтервал
4) E = (a, b] = {xЄR, a<x≤b} – полуинтервал
5) E = (-∞, a] = {xЄR, -∞<x≤a} – бесконечный полуинтервал
6) E = (-∞, a) = {xЄR, -∞<x<a} – бесконечный полуинтервал
7) E = [b, +∞) = {xЄR, b≤x<+∞} – бесконечный полуинтервал
8) E = (b, +∞) = { xЄR, b<x<+∞} – бесконечный полуинтервал
Интервал вида (x0-ε, x0+ε), где ε-любое положительное число, назыв. эпсилон-окрестностью точки x0, а x0 – центр этой ε-окр-ти.
Если xЄ(x0-ε, x0+ε), то x0-ε<x<x0+ε. => -ε<x-x0<+ε => |x-x0|<ε – x принадлежит ε-окр-ти в точке x0.
3. Ограниченные числовые множества, точные грани множеств.
Пусть EcR.
Опред.1: если для рассматриваемого мн-ва Е существует такое действит. число М, что все элементы данного мн-ва удовлетв. условию х≤М, то говорят, что мн-во Е ограниченного сверху, а число М назыв. верхней границей мн-ва Е
(ƎМϵR)( xϵE):x≤M
xϵE):x≤M
Опред.2: мн-во Е назыв. ограниченным снизу, если существует такое действит. число m, что все эл-ты данного мн-ва удовлетв. условию x≥m
(ƎmϵR)( xϵE): x≥m
xϵE): x≥m
Опред.3: мн-во Е назыв. ограниченным, если оно ограниченно сверху и снизу одновременно
(ƎМϵR, ƎmϵR)( xϵE):m≤x≤M
xϵE):m≤x≤M
Если мн-во огранич. сверху, то оно имеет бесконечное мн-во верхних границ. Среди них выдел. наим. верхнюю границу, т.е. границу, которая ближе всех к мн-ву.
Опред.4: наим. из всех верхних границ М назыв. точной верхней гранью мн-ва Е, если она удовлетворяет следующим условиям:
1) ( xϵE):x≤M
xϵE):x≤M
2) ( ε>0)(ƎxεϵE):M-ε<xε≤M
ε>0)(ƎxεϵE):M-ε<xε≤M
M=sup – точная верхняя граница
Если мн-во ограничено снизу, оно имеет бесконечно много нижних границ. Среди мн-ва нижних выбирают ту, которая ближе подходит к мн-ву. Ее назыв. точной нижней границей.
Опред.5: наиб. из всех нижних границ m назыв. точной нижней гранью. Число m явл. точной нижней границей, если для него выполн. след. правила:
1) ( xϵE): x≥m
xϵE): x≥m
2) ( ε>0)(ƎxεϵE):x<m+ε
ε>0)(ƎxεϵE):x<m+ε
m=inf – точная нижняя граница
Теор: Всякое огранич. снизу мн-во имеет точную нижнюю границу, всякое огранич. сверху мн-во имеет точную верхнюю границу. Если мн-во Е не ограничено сверху, то за его точную верхнюю границу берут +∞. Если мн-во Е не ограничено снизу, то за его точную нижнюю границу берут -∞.
4. Опред.: пусть даны два непустых мн-ва EcR и YcR. Закон f, по которому каждому эл-ту xϵE ставится в соответствие один и только один эл-нт yϵY назыв. функцией или отображением мн-ва Е на мн-во Y и обозначается y=f(x) или f:E→Y.
Мн-во Е назыв. областью определения ф-ии, а мн-во Y – мн-вом значений. При этом х назыв. аргументом или независимой переменной, а y – функцией или завис. переменной.
Если обл. опред. не указана. То она совпадает со мн-вом допустимых значений.
Основные свойства функций.
Опред.1: пусть ф-я y=f(x) определена на симметричном мн-ве [-a, a] (или (-а, а)). f(x) четная на мн-ве Е, если ( xϵE):f(-x)=f(x)
xϵE):f(-x)=f(x)
f(x) нечетная на мн-ве Е, если ( xϵE):f(-x)=-f(x)
xϵE):f(-x)=-f(x)
Опред.2: пусть ф-я y=f(x) определена на мн-ве Е. если ( x1, x2ϵE):x1<x2 выполн. Нерав-ва:
x1, x2ϵE):x1<x2 выполн. Нерав-ва:
1) f(x1)<f(x2) – f(x)-монотонно-возрастающая на мн-ве Е
2) f(x1)≤f(x2) – f(x)-неубывающая на мн-ве Е
3) f(x1)>f(x2) – f(x)-монотонно-убывающая на мн-ве Е
4) f(x1)≥f(x2) – f(x)-невозрастающая на мн-ве Е
Опред.3: ф-я y=f(x) назыв. ограниченной на мн-ве Е, если мн-во ее значений (Y) ограниченно на мн-ве Е.
(ƎmϵR)(ƎMϵR)( xϵE):m≤f(x)≤M/ в противном случае ф-я назыв. неограниченной.
xϵE):m≤f(x)≤M/ в противном случае ф-я назыв. неограниченной.
Опред.4: число М назыв точной верхней гранью ф-и на мн-ве Е, если вып. след. усл-я:
1) (ƎMϵR)( xϵE):f(x)≤M
xϵE):f(x)≤M
2) ( ε>0)(ƎxεϵE):f(xε)>M-ε
ε>0)(ƎxεϵE):f(xε)>M-ε
и обозначают M=supf(x), xϵЕ
Опред.5: число m назыв. точной нижней границей ф-и f(x) на мн-ве Е, если вып.след.усл-я:
1) (ƎmϵR)( xϵE):f(x)≥m
xϵE):f(x)≥m
2) ( ε>0)(ƎxεϵE):f(xε)<m+ε
ε>0)(ƎxεϵE):f(xε)<m+ε
и обозначают m=inff(x), xϵE.
Ф-я y=f(x) назыв. периодической на мн-ве Е, если (ƎT>0, TϵR) ( xϵE):f(x+T)=f(x), где Т-период ф-и.
xϵE):f(x+T)=f(x), где Т-период ф-и.
Если Т-период, то mT, m=±1. ±2, … - периоды f(x)/ за основной период ф-и принимают наименьшее положит число.
y=sinX. ±2П,±4П, ±6П – периоды. Т=2П – основной период
5. Обратные функции.
Опред.: пусть на мн-ве Е задана ф-я y=f(x) и Y-ее мн-во значений. Если каждому эл-ту yϵY по закону g ставится в соответствие единственное число xϵE, то говорят, что на мн-ве Е задана обратная ф-я и обозначают x=g(y)=f-1(x). Ф-ю y=f(x) назыв. прямой ф-ей.
y=f(x), E – обл. опред., Y – мн-во знач.
x=g(y), Y – обл. опред., E – мн-во знач.
Понятие сложной функции.
Опред.: пусть ф-я y=f(x) определена при uϵD, а ф-я u=φ(x) определена на мн-ве Е(xϵE), причем ( xϵE): u=φ(x)ϵD. Тогда говорят, что на мн-ве Е задана ф-я y=(φ(x)), которая назыв. сложной ф-ей или суперпозицией ф-й, при этом обл. опред. сложной ф-и будем назыв. мн-во значений х, при которых определяется ф-и f и ф и мн-во знач. Ф-й ф(х) явл. обл. опред. ф-и f.
xϵE): u=φ(x)ϵD. Тогда говорят, что на мн-ве Е задана ф-я y=(φ(x)), которая назыв. сложной ф-ей или суперпозицией ф-й, при этом обл. опред. сложной ф-и будем назыв. мн-во значений х, при которых определяется ф-и f и ф и мн-во знач. Ф-й ф(х) явл. обл. опред. ф-и f.
6. Опред.1:Пусть EϵR – произвольное непустое мн-во. Отображение f мн-ва натер. чисел на мн-во Е назыв. числовой последовательностью и обозначается xn=f(n), т.е. числовая послед-ть – ф-я натурального элемента.
Для числовой последовательности важно, что это бесконечное мн-во, т.е. числ. послед-ть содержит бесконечное число эл-тов.
Числ. послед-ть – это упорядоченное мн-во, т.к. эл-ты данного мн-ва следуют в порядке возрастания n. При этом эл-нт xn стоит за xn-1 и перед xn+1.
Опред.2: Число aϵR назыв. пределом числ. послед-ти xn, если для каждого положительного числа ε, сколь бы мало оно не было, существует такой номер N(ε)ϵN, что все эл-ты послед-ти xn, номера которого n> N(ε) удовлетворяет неравенству |xn-a|<ε.
( ε>0)(Ǝ N(ε)ϵN)((
ε>0)(Ǝ N(ε)ϵN)(( nϵN, n> N(ε)):|xn-a|<ε
nϵN, n> N(ε)):|xn-a|<ε
И тот факт, что a явл. членом числ. послед-ти  n=а или xn→a. Числовая послед-ть в этом случае назыв. сходящейся. Если указанный предел не существует или равен ∞, то числ. послед-ть назыв расходящейся.
n=а или xn→a. Числовая послед-ть в этом случае назыв. сходящейся. Если указанный предел не существует или равен ∞, то числ. послед-ть назыв расходящейся.
Если ε уменьшается, то номер N(ε)-увеличивается. И в любой сколь угодно малой окр-ти лежит бесконечное число эл-тов.
Точка а – предельная точка(точка сгущения).
Если номер N(ε) – отриц., это означает, что все эл-ты послед-ти лежат в выбранной ε-окр-ти точки а.
7. Если числовая послед-ть сходится, то она сходится к единственному пределу.
Док-во: методом от противного. Предпол., что числ. послед-ть сходится к двум различным пределам. Пусть Ǝ  n=а ó (
n=а ó ( ε>0)(Ǝ N1(ε)ϵN)(
ε>0)(Ǝ N1(ε)ϵN)( nϵN, n> N1(ε)):|xn-a|<ε (1)
nϵN, n> N1(ε)):|xn-a|<ε (1)
и пусть  n=а` ó (
n=а` ó ( ε>0)(Ǝ N2(ε)ϵN)((
ε>0)(Ǝ N2(ε)ϵN)(( nϵN, n> N2(ε)):|xn-a`|<ε (2), причем a≠a`. Т.к. в определении предела ε любое, то выберем его таким, чтобы ε-окр-ти чисел a и a` не пересекались.
nϵN, n> N2(ε)):|xn-a`|<ε (2), причем a≠a`. Т.к. в определении предела ε любое, то выберем его таким, чтобы ε-окр-ти чисел a и a` не пересекались.
Выберем N(ε) равное максимальному { N1(ε), N2(ε)}. Тогда при любых n> N(ε)определения (1) и (2) выполняются одновременно.
Геометрический смысл определения: начиная с некоторого номера все элементы лежат в ε-окр-ти этой точки. След-но при n>N(ε) все элементы послед-ти лежат в ε-окр-ти точки а и ε-окр-ти точки а`, что является невозможным => a=a`, т.е. послед-ть сходится к единственному пределу.
Опред.: числ. послед-ть назыв. ограниченной, если мн-во значений ее ограниченно, т.е. (ƎmϵR)(ƎMϵR)( nϵN):m≤x≤M/ или определение огранич-ой послед-ти можно записать так: (ƎM>0)(
nϵN):m≤x≤M/ или определение огранич-ой послед-ти можно записать так: (ƎM>0)( nϵN):|xn|≤M.
nϵN):|xn|≤M.
8. Если числ. послед-ть сходится, то она ограничена.
Док-во: Пусть xn сходится, т.е.  n=а ó (
n=а ó ( ε>0)(ƎN(ε)ϵN)(
ε>0)(ƎN(ε)ϵN)( nϵN, n> N(ε)):|xn-a|<ε. Выберем число M~=max{ε, |x1-a|, |x2-a|,…, |xn-a|}ю тогда при
nϵN, n> N(ε)):|xn-a|<ε. Выберем число M~=max{ε, |x1-a|, |x2-a|,…, |xn-a|}ю тогда при  nϵN будет выполнятся неравенство |xn-a|≤M~ => -M~≤ xn-a≤M~ или a-M~≤xn≤a+M~ (a-M~=m, a+M~=M)
nϵN будет выполнятся неравенство |xn-a|≤M~ => -M~≤ xn-a≤M~ или a-M~≤xn≤a+M~ (a-M~=m, a+M~=M)
(Ǝm=a-M~)(ƎM=a+M~)( nϵN):m≤xn≤M. это означает, что числ. послед-ть ограничена.
nϵN):m≤xn≤M. это означает, что числ. послед-ть ограничена.
9. Если xn и yn-сходящиеся числ. послед-ти, т.е.  n=x,
n=x, 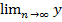 n=y, то:
n=y, то:
1) 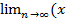 n ± yn) =
n ± yn) =  n ±
n ± 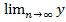 n = x ± y
n = x ± y
Док-во: докажем, что 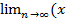 n + yn) = x + y
n + yn) = x + y
Т.к. xn→x ó ( ε>0)(Ǝ N1(ε)ϵN)(
ε>0)(Ǝ N1(ε)ϵN)( nϵN, n> N1(ε)):|xn-x|<ε/2 (1)
nϵN, n> N1(ε)):|xn-x|<ε/2 (1)
Т.к. yn→y ó ( ε>0)(Ǝ N2(ε)ϵN)((
ε>0)(Ǝ N2(ε)ϵN)(( nϵN, n> N2(ε)):|yn-y|<ε/2 (2).
nϵN, n> N2(ε)):|yn-y|<ε/2 (2).
Выберем N(ε)=max{ N1(ε), N2(ε)}. Тогда при  n>N(ε) опред-я (1) и (2) выполняются одновременно.
n>N(ε) опред-я (1) и (2) выполняются одновременно.
Оценим разность при  n> N(ε): |(xn+yn)-(x+y)| = |(xn-x)+(yn-y)|≤|xn-x|+|yn-y|< ε/2 + ε/2 = ε
n> N(ε): |(xn+yn)-(x+y)| = |(xn-x)+(yn-y)|≤|xn-x|+|yn-y|< ε/2 + ε/2 = ε
Получено следующее определение: ( ε>0)(ƎN(ε)ϵN)(
ε>0)(ƎN(ε)ϵN)( nϵN, n> N(ε)): |(xn+yn)-(x+y)|< ε
nϵN, n> N(ε)): |(xn+yn)-(x+y)|< ε
Это означает, что 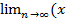 n + yn) = x + y. Ч.т.д.
n + yn) = x + y. Ч.т.д.
Док-во: докажем, что 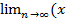 n - yn) = x - y
n - yn) = x - y
Т.к. xn→x ó ( ε>0)(Ǝ N1(ε)ϵN)(
ε>0)(Ǝ N1(ε)ϵN)( nϵN, n> N1(ε)):|xn-x|<ε/2 (1)
nϵN, n> N1(ε)):|xn-x|<ε/2 (1)
Т.к. yn→y ó ( ε>0)(Ǝ N2(ε)ϵN)((
ε>0)(Ǝ N2(ε)ϵN)(( nϵN, n> N2(ε)):|yn-y|<ε/2 (2).
nϵN, n> N2(ε)):|yn-y|<ε/2 (2).
Выберем N(ε)=max{N1(ε), N2(ε)}. Тогда при  n>N(ε) опред-я (1) и (2) выполняются одновременно.
n>N(ε) опред-я (1) и (2) выполняются одновременно.
Оценим разность при  n> N(ε): |(xn-yn)-(x-y)| = |(xn-x)-(yn-y)|≤|xn-x|-|yn-y|< ε/2 + ε/2 = ε
n> N(ε): |(xn-yn)-(x-y)| = |(xn-x)-(yn-y)|≤|xn-x|-|yn-y|< ε/2 + ε/2 = ε
Получено следующее определение: ( ε>0)(ƎN(ε)ϵN)(
ε>0)(ƎN(ε)ϵN)( nϵN, n> N(ε)): |(xn-yn)-(x-y)|< ε
nϵN, n> N(ε)): |(xn-yn)-(x-y)|< ε
Это означает, что 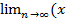 n - yn) = x - y. Ч.т.д.
n - yn) = x - y. Ч.т.д.
2) 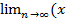 n*yn) =
n*yn) =  n *
n * 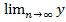 n = xy
n = xy
Т.к. xn→x ó ( ε>0)(Ǝ N1(ε)ϵN)(
ε>0)(Ǝ N1(ε)ϵN)( nϵN, n> N1(ε)):|xn-x|<ε (1)
nϵN, n> N1(ε)):|xn-x|<ε (1)
Т.к. yn→y ó ( ε>0)(Ǝ N2(ε)ϵN)((
ε>0)(Ǝ N2(ε)ϵN)(( nϵN, n> N2(ε)):|yn-y|<ε (2).
nϵN, n> N2(ε)):|yn-y|<ε (2).
Выберем N(ε)=max{ N1(ε), N2(ε)}. Тогда при  n>N(ε) опред-я (1) и (2) выполняются одновременно.
n>N(ε) опред-я (1) и (2) выполняются одновременно.
Оценим разность |(xn*yn)-(xy)| при  n> N(ε)
n> N(ε)
|xn*yn-xy| = |(xn-x)*(yn-y)+xyn+xny-2xy| = |(xn-x)(yn-y)+x(yn-y)+y(xn-x)|≤ |(xn-x)*(yn-y)|+| x(yn-y)|+|y(xn-x)| = |xn-x|*|yn-y|+|x|*|xn-x|+|y|*|yn-y|<ε2+|x|*ε+|y|*ε = ε1
Получаем следующее определение: ( ε1>0)(ƎN(ε1)ϵN(ε))(
ε1>0)(ƎN(ε1)ϵN(ε))( nϵN, n> N(ε1)): |xn*yn-xy|< ε1
nϵN, n> N(ε1)): |xn*yn-xy|< ε1
Это означает, что 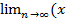 n*yn) = xy ч.т.д.
n*yn) = xy ч.т.д.
3) 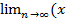 n/yn) =
n/yn) =  n /
n / 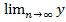 n = x/y, yn≠0, y≠0
n = x/y, yn≠0, y≠0
Сначала докажем, что 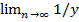 n = 1/y
n = 1/y
Т.к. yn→y ó ( ε>0)(Ǝ N1(ε)ϵN)(
ε>0)(Ǝ N1(ε)ϵN)( nϵN, n> N1(ε)):|yn-y|<ε (1)
nϵN, n> N1(ε)):|yn-y|<ε (1)
Т.к. начиная с номера N1(ε) все эл-ты послед-ти yn лежат в ε-окр-ти точки y, то они все будут удовлетворять следующему неравенству: |y1|>|y|/2 при  n> N2(ε)
n> N2(ε)
Выберем за N(ε)=max{N1(ε), N2(ε)} и при  n> N(ε) оценим разность: |1/y – 1/yn| = |(y-yn)/y*yn| = |y-yn|/|yn|*|y| < |yn-y|/(|y|/2)*|y| = 2|yn-y|/|y|*|y| < 2 ε/|y|2 = ε1 => =>
n> N(ε) оценим разность: |1/y – 1/yn| = |(y-yn)/y*yn| = |y-yn|/|yn|*|y| < |yn-y|/(|y|/2)*|y| = 2|yn-y|/|y|*|y| < 2 ε/|y|2 = ε1 => => 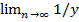 n = 1/y
n = 1/y
Рассмотрим 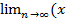 n/yn) =
n/yn) = 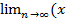 n * 1/yn) = x * 1/y = x/y Ч.т.д.
n * 1/yn) = x * 1/y = x/y Ч.т.д.
10. пусть даны числ. послед-ти xn, yn, zn
1) для сходящихся числ. послед-тей xn и yn из соотношения  n=x,
n=x, 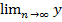 n=y и xn≤yn (
n=y и xn≤yn ( nϵN) следует, что x≤y
nϵN) следует, что x≤y
Док-во: Т.к. xn→x ó ( ε>0)(Ǝ N1(ε)ϵN)(
ε>0)(Ǝ N1(ε)ϵN)( nϵN, n> N1(ε)):|xn-x|<ε/2 (1)
nϵN, n> N1(ε)):|xn-x|<ε/2 (1)
Т.к. yn→y ó ( ε>0)(Ǝ N2(ε)ϵN)((
ε>0)(Ǝ N2(ε)ϵN)(( nϵN, n> N2(ε)):|yn-y|<ε/2 (2)
nϵN, n> N2(ε)):|yn-y|<ε/2 (2)
N(ε)=max{N1(ε), N2(ε)} и при  n> N(ε) опред-я (1) и (2) выполняются одновременно.
n> N(ε) опред-я (1) и (2) выполняются одновременно.
Предположим методом от противного, что x>y и выберем ε = x-y.
(1): x- ε/2<xn< x+ε/2 => xn≥ x- ε/2 = (ε+y)- ε/2 = y+ ε/2>yn
(2): y- ε/2<yn<y+ ε/2
Это противоречит условию xn≤yn  nϵN. След-но предположение что x>y неверно.
nϵN. След-но предположение что x>y неверно.
2) Из соотношений  n =
n = 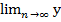 n = a и xn≤zn≤yn следует, что
n = a и xn≤zn≤yn следует, что 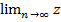 n = a
n = a
Док-во: Т.к. xn→a ó ( ε>0)(Ǝ N1(ε)ϵN)(
ε>0)(Ǝ N1(ε)ϵN)( nϵN, n> N1(ε)):|xn-a|<ε (1)
nϵN, n> N1(ε)):|xn-a|<ε (1)
yn→a ó ( ε>0)(Ǝ N2(ε)ϵN)(
ε>0)(Ǝ N2(ε)ϵN)( nϵN, n> N2(ε)):|yn-a|<ε (2)
nϵN, n> N2(ε)):|yn-a|<ε (2)
N(ε)=max{N1(ε), N2(ε)} и при  n> N(ε) опред-я (1) и (2) выполняются одновременно.
n> N(ε) опред-я (1) и (2) выполняются одновременно.
(1): a- ε<xn< a+ε => a- ε<xn≤zn≤yn< a+ ε  n>N(ε)
n>N(ε)
(2): a- ε<yn<a+ ε
Получаем a- ε< zn< a+ ε  n>N(ε) => (
n>N(ε) => ( ε>0)(Ǝ N(ε)ϵN)(
ε>0)(Ǝ N(ε)ϵN)( nϵN, n> N(ε)):|zn-a|<ε => =>
nϵN, n> N(ε)):|zn-a|<ε => => 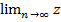 n=a
n=a
11. Опред.1: последовательность xn называется бесконечно малой, если  n=0 ó ó (
n=0 ó ó ( ε>0)(ƎN(ε)ϵN)(
ε>0)(ƎN(ε)ϵN)( nϵN, n> N(ε)):|xn|<ε.
nϵN, n> N(ε)):|xn|<ε.
Смысл б.м. послед-ти: каково бы ни было сколь угодно малое положительное число ε, всегда найдется такой номер N(ε), начиная с которого все эл-ты послед-ти лежат вблизи нуля (в малой ε-окр-ти).
Опред.2: числ. послед-ть xn назыв. Бесконечно большой, если  n=∞ ó ó (
n=∞ ó ó ( ε>0)(Ǝ N(ε)ϵN)(
ε>0)(Ǝ N(ε)ϵN)( nϵN, n> N(ε)):|xn|>ε.
nϵN, n> N(ε)):|xn|>ε.
Смысл б.б. послед-ти: каково бы ни было сколь угодно большое положительное число ε, всегда найдется номер N(ε), начиная с которого все эл-ты послед-ти по модулю становятся больше заданного большого числа ε.
Если xn>0, xn – б.б. ó ( ε>0)(Ǝ N(ε)ϵN)(
ε>0)(Ǝ N(ε)ϵN)( nϵN, n> N(ε)):xn>ε.
nϵN, n> N(ε)):xn>ε.
Если xn<0, xn - б.б. ó ( ε>0)(Ǝ N(ε)ϵN)(
ε>0)(Ǝ N(ε)ϵN)( nϵN, n> N(ε)):xn<-ε.
nϵN, n> N(ε)):xn<-ε.
Связь между б.б. и б.м. послед-ми.
Если xn – б.м., то 1/xn – б.б. и наоборот.
Док-во: пусть xn – б.м. ó ( ε>0)(ƎN(ε)ϵN)(
ε>0)(ƎN(ε)ϵN)( nϵN, n> N(ε)):|xn|<ε.
nϵN, n> N(ε)):|xn|<ε.
|xn|< ε умножим на 1/(|xn|*ε) => 1/ε<1/|xn| => 1/|xn|>1/ε  nϵN.
nϵN.
( 1/ε>0)(Ǝ N(ε)ϵN)(
1/ε>0)(Ǝ N(ε)ϵN)( nϵN, n> N(ε)):1/|xn|>1/ε => 1/xn – б.б.
nϵN, n> N(ε)):1/|xn|>1/ε => 1/xn – б.б.
Свойства б.м. послед-тей.
1) Сумма или разность двух б.м. послед-тей есть величина б.м.
Пусть xn, yn – б.м., т.е.  n=0,
n=0, 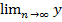 n=0
n=0
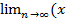 n ± yn) =
n ± yn) =  n ±
n ± 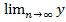 n = 0 => (x ± y) – б.м.
n = 0 => (x ± y) – б.м.
2) Произведение двух б.м. послед-тей есть б.м. послед-ть
Док-во аналогично. Св-ва 1 и 2 обобщаются на конечное число б.м. послед-тей.
3) Произведение б.м. послед-ти на ограниченную есть величина б.м.
Док-во: пусть zn=xn*yn, где xn – ограниченная послед-ть, т.е. (ƎM>0)( nϵN):|xn|≤M
nϵN):|xn|≤M
Пусть yn – б.м. => ( ε>0)(ƎN(ε)ϵN)(
ε>0)(ƎN(ε)ϵN)( nϵN, n> N(ε)):|yn|< ε/M.
nϵN, n> N(ε)):|yn|< ε/M.
Оценим |xn*yn| при  n>N(ε): |xn*yn|=|xn|*|yn|≤M*|yn|(
n>N(ε): |xn*yn|=|xn|*|yn|≤M*|yn|( nϵN)<M*(ε/M) = ε (
nϵN)<M*(ε/M) = ε ( nϵN) => => zn=xn*yn – б.м.
nϵN) => => zn=xn*yn – б.м.
12. Монотонные последовательности.
Опред.: послед-ть xn назыв.: 1) монот.-возраст, ( n1, n2ϵN)(n1<n2):xn1<xn2
n1, n2ϵN)(n1<n2):xn1<xn2
2) неубывающей, ( n1, n2ϵN)(n1<n2):xn1≤xn2
n1, n2ϵN)(n1<n2):xn1≤xn2
3) монот.-убыв, ( n1, n2ϵN)(n1<n2):xn1>xn2
n1, n2ϵN)(n1<n2):xn1>xn2
4) невозрастающей, ( n1, n2ϵN)(n1<n2):xn1≥xn2
n1, n2ϵN)(n1<n2):xn1≥xn2
Теорема о пределе монот.-возраст. послед-ти.
Всякая монот.-возраст. послед-ть, ограниченная сверху, имеет предел, равный точной верхней грани послед-ти.
Всякая монот.-возраст. послед-ть, не ограниченная сверху, имеет предел, равный +∞.
Док-во: пусть xn – монот.-возраст. и ограниченна сверху. Всякое огранич. сверху мн-во имеет точную верхнюю грань, т.е. существует M=sup xn ó (ƎMϵR)( nϵN):xn≤M (1)
nϵN):xn≤M (1)
( ε>0)(Ǝ N(ε)ϵN):xN(ε)>M-ε (2).
ε>0)(Ǝ N(ε)ϵN):xN(ε)>M-ε (2).
Т.к. xn – монот.-возраст., то  n> N(ε):xn> xN(ε)>M- ε => M-ε<xn≤M<M+ ε => M-ε<xn<M+ε для (
n> N(ε):xn> xN(ε)>M- ε => M-ε<xn≤M<M+ ε => M-ε<xn<M+ε для ( n> N(ε) => |xn-M|< ε для (
n> N(ε) => |xn-M|< ε для ( n> N(ε) => (
n> N(ε) => ( ε>0)(ƎN(ε)ϵN)(
ε>0)(ƎN(ε)ϵN)( nϵN, n>N(ε)): |xn-M|< ε ó ó
nϵN, n>N(ε)): |xn-M|< ε ó ó  n=M ч.т.д.
n=M ч.т.д.
Пусть xn – монот.-возраст. и не ограниченна сверху: (ƎMϵR)( nϵN):xn<M
nϵN):xn<M
( ε>0)(Ǝ N(ε)ϵN):xN(ε)>ε
ε>0)(Ǝ N(ε)ϵN):xN(ε)>ε
Т.к. xn – монот.-возраст, то  n> N(ε):xn> xN(ε)>ε
n> N(ε):xn> xN(ε)>ε
Получено след. опред: ( ε>0)(ƎN(ε)ϵN)(
ε>0)(ƎN(ε)ϵN)( nϵN, n>N(ε)): xn>ε =>
nϵN, n>N(ε)): xn>ε =>  n=+∞. Ч.т.д.
n=+∞. Ч.т.д.
Теорема о пределе монот.-убыв. послед-ти.
Если послед-ть монот.-убыв. и ограничена снизу, то она имеет предел, равный точной нижней грани послед-ти.
Предел монот.-убыв. послед-ти, неограниченной снизу, равен -∞.
Док-во: пусть xn-монот.-убыв. и ограничена снизу. Всякое огранич. снизу мн-во имеет точную нижнюю грань, т.е. существует m=inf xn ó (ƎmϵR)( nϵN):xn≥m (1)
nϵN):xn≥m (1)
( ε>0)(Ǝ N(ε)ϵN):xN(ε)<m+ε (2).
ε>0)(Ǝ N(ε)ϵN):xN(ε)<m+ε (2).
Т.к. xn – монот.-убыв., то  n> N(ε):xn< xN(ε)<m+ε => m-ε<m≤ xn<m+ε => m-ε<xn<m+ε для
n> N(ε):xn< xN(ε)<m+ε => m-ε<m≤ xn<m+ε => m-ε<xn<m+ε для  n> N(ε) => |xn-m|<ε => для
n> N(ε) => |xn-m|<ε => для  n> N(ε) => (
n> N(ε) => ( ε>0)(ƎN(ε)ϵN)(
ε>0)(ƎN(ε)ϵN)( nϵN, n>N(ε)): |xn-m|<ε ó ó
nϵN, n>N(ε)): |xn-m|<ε ó ó  n=m ч.т.д.
n=m ч.т.д.
Пусть xn – монот.-убыв. и не ограничена снизу: (ƎmϵR)( nϵN):xn≥m
nϵN):xn≥m
( ε>0)(ƎN(ε)ϵN):xN(ε)<ε
ε>0)(ƎN(ε)ϵN):xN(ε)<ε
Т.к. xn – монот.-убыв. послед-ть, то  n> N(ε):xn<xN(ε)<ε
n> N(ε):xn<xN(ε)<ε
Получено след. опред.:: ( ε>0)(ƎN(ε)ϵN)(
ε>0)(ƎN(ε)ϵN)( nϵN, n>N(ε)): xn<ε =>
nϵN, n>N(ε)): xn<ε =>  n=-∞. Ч.т.д.
n=-∞. Ч.т.д.
13. Второй замечательный предел.
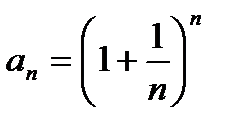 = 1+n * (1/n) + (n(n-1))/2! * (1/n2)+(n(n-1)(n-2))/3! * (1/n3) +…+ (n(n-1)(n-2)…*2*1)/n! * (1/nn)
= 1+n * (1/n) + (n(n-1))/2! * (1/n2)+(n(n-1)(n-2))/3! * (1/n3) +…+ (n(n-1)(n-2)…*2*1)/n! * (1/nn)
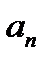 = 2+1/2*(1-1/n) + 1/3!*(1-1/n)(1-2/n) +…+ 1/n!*(1-1/n)(1-2/n)…(1-(n-1)/n)
= 2+1/2*(1-1/n) + 1/3!*(1-1/n)(1-2/n) +…+ 1/n!*(1-1/n)(1-2/n)…(1-(n-1)/n)
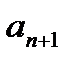 = (1-1/(n+1))n+1=2 + 1/2*(1-1/(n+1)) + 1/3!*(1-1/(n+1))(1-2/(n+1)) +…+ 1/n!*(1-1/(n+1))(1-2/(n+1))…(1-(n-1)/(n+1)) + 1/(n+1)!*(1-1/(n+1))(1-2/(n+1))…(1-n/(n+1))
= (1-1/(n+1))n+1=2 + 1/2*(1-1/(n+1)) + 1/3!*(1-1/(n+1))(1-2/(n+1)) +…+ 1/n!*(1-1/(n+1))(1-2/(n+1))…(1-(n-1)/(n+1)) + 1/(n+1)!*(1-1/(n+1))(1-2/(n+1))…(1-n/(n+1))
Сравним 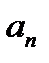 и
и 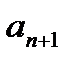 : 1/2*(1-1/n) < 1/2*(1-1/(n+1))
: 1/2*(1-1/n) < 1/2*(1-1/(n+1))
1/3!*(1-1/n)(1-2/n) < 1/3!*(1-1/n+1)(1-2/(n+1)) …
1/n!*(1-1/n)(1-2/n)…(1-(n-1)/n) < 1/n!*(1-1/(n+1))(1-2/(n+1))…(1-(n-1)/(n+1))
В 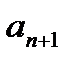 есть дополнительное положительное слагаемое 1/(n+1)!*(1-1/(n+1))(1-2/(n+1))…(1-n/(n+1)), поэтому
есть дополнительное положительное слагаемое 1/(n+1)!*(1-1/(n+1))(1-2/(n+1))…(1-n/(n+1)), поэтому 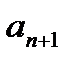 >
> 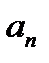 . Т.к.
. Т.к. 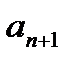 >
> 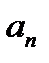 , то послед-ть монот. Возрастает.
, то послед-ть монот. Возрастает.
Теперь докажем, что 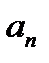 ограничена сверху.
ограничена сверху.
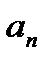 = 2 + 1/2*(1-1/n) + 1/3!*(1-1/n)(1-2/n) +…+ 1/n!*(1-1/n)(1-2/n)…(1-(n-1)/n) < 2 + 1/2 + 1/3! + 1/4!+ +…+ 1/n! < 2 + 1/2 + 1/22 + 1/23 +…+ 1/2n-1 = 1 + (1 + 1/2 + 1/22 + 1/23 +…+ 1/2n-1) = 1 + (1-(1/2)n/(1-1/2) = 1 + 2(1-(1/2)n) = 3-1/(2n-1) < 3
= 2 + 1/2*(1-1/n) + 1/3!*(1-1/n)(1-2/n) +…+ 1/n!*(1-1/n)(1-2/n)…(1-(n-1)/n) < 2 + 1/2 + 1/3! + 1/4!+ +…+ 1/n! < 2 + 1/2 + 1/22 + 1/23 +…+ 1/2n-1 = 1 + (1 + 1/2 + 1/22 + 1/23 +…+ 1/2n-1) = 1 + (1-(1/2)n/(1-1/2) = 1 + 2(1-(1/2)n) = 3-1/(2n-1) < 3
Т.е. послед-ть xn – ограничена сверху и по теореме существует предел 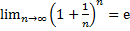 .
.
14. 1) 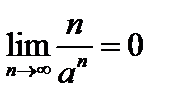 , (
, (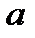 >1)
>1)
Xn = 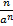 >0 – послед-ть, огранич. снизу
>0 – послед-ть, огранич. снизу
Xn+1 = 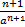
Xn+1 / Xn = 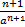 *
* 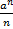 =
= 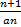 < 1 => n+1 < an =>(a-1)n > 1 => n >
< 1 => n+1 < an =>(a-1)n > 1 => n > 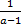
Xn – монот.-убывает при n > 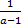 и ограничена снизу(по теореме)
и ограничена снизу(по теореме)
Существует предел  n = A
n = A
Xn+1 = 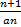 * xn (A=1/a * A) |*
* xn (A=1/a * A) |* 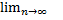 => A=1/a * A => A=0. Следовательно
=> A=1/a * A => A=0. Следовательно 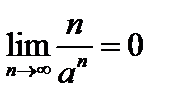 . ч.т.д.
. ч.т.д.
2) 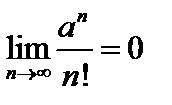 , (
, (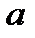 >1)
>1)
Xn = 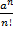 – послед-ть ограничена снизу
– послед-ть ограничена снизу
Xn+1 = 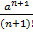
Xn+1 / Xn = 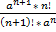 =
= 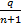 < 1 => a < n+1 => n > a-1
< 1 => a < n+1 => n > a-1
Xn – монот.-убывает при n > a-1 и ограничена снизу(по теореме)
Существует предел  n = A
n = A
Xn+1 = 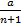 * xn (A=0 * A) |*
* xn (A=0 * A) |* 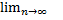 => A=0. Следовательно
=> A=0. Следовательно 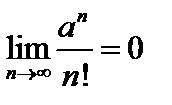 . Ч.т.д.
. Ч.т.д.
3) 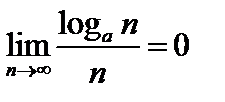
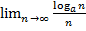 =
= 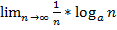 =
= 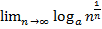 =
= 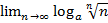 =
= 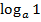 = 0
= 0
4) 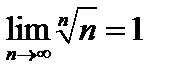
xn = 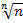 – 1 (n>1). Число n представимо в виде n = (
– 1 (n>1). Число n представимо в виде n = (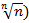 n = (1 + (
n = (1 + (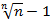 ))n = 1 + n(
))n = 1 + n(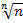 –1)+ +
–1)+ + 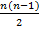 * (
* (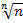 – 1)2 +
– 1)2 + 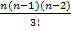 * (
* (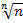 – 1)3 + … + (
– 1)3 + … + (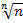 – 1)n >
– 1)n > 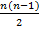 * (
* (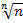 – 1)2
– 1)2
n > 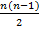 * (
* (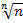 – 1)2 => (
– 1)2 => (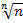 – 1)2 <
– 1)2 < 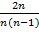 =>
=> 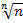 – 1 >
– 1 > 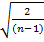 |*
|* 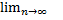 => по теореме о зажатой послед-ти
=> по теореме о зажатой послед-ти  n=0.
n=0.
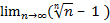 =
= 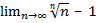 = 0 =>
= 0 => 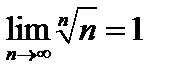
Ч.т.д.
15. Опред.: пусть задана числ. послед-ть xn. Из натур. мн-ва чисел выберем послед. номеров n1<n2<n3<…<nk<…. Тогда эл-ты послед-ти xn с номерами xn1, xn2, …, xnk, … образуют подпоследовательность или частичную послед-ть для послед-ти xn. Если подпослед-ть сходится, то ее предел назыв. частичным пределом.
Пример: xn=  – числ. послед-ть { xn,
– числ. послед-ть { xn,  ,
,  , …,
, …,  , …}
, …}
{x2n} = {  ,
,  , …,
, …, 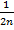 , …} частичные послед-ти (подпослед-ти) для xn=
, …} частичные послед-ти (подпослед-ти) для xn= 
{x2n+1} = {1,  ,
,  , …,
, …, 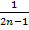 , …}
, …}
{xn} = {1,  ,
,  ,
,  ,
,  , …,
, …, 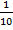 , …}
, …}
Подпослед-ти можно выбирать любыми способами.
Теоремы о подпоследовательностях.
Теор.1: для того чтобы числ. послед-ть имела своим пределом число a, необходимо и достаточно, чтобы любая ее подпослед-ть xnk сходилась к числу a(без док-ва).
Теор.2: если послед-ть xn имеет две подпослед-ти, сходящиеся к разным пределам, то данная послед-ть xn разходится.
Док-во: xnk→a при nk→∞ и xnm→и при nm→∞ и a≠b
( ε>0)(Ǝ N1(ε)ϵN)(
ε>0)(Ǝ N1(ε)ϵN)( nϵN, n> N1(ε)):|xnk-a|<ε (1)
nϵN, n> N1(ε)):|xnk-a|<ε (1)
( ε>0)(Ǝ N2(ε)ϵN)(
ε>0)(Ǝ N2(ε)ϵN)( nϵN, n> N2(ε)):|xnm-b|<ε (2)
nϵN, n> N2(ε)):|xnm-b|<ε (2)
Выберем ε таким, чтобы ε-окр-ти a и b не пересекались. N(ε)=max{N1(ε), N2(ε)}.
Тогда при nk> N(ε) и nm> N(ε) определения (1) и (2) выполняются одновременно. Отсюда следует, что 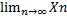 не существует.
не существует.
Замечание: понятие подпослед-ти и частичной послед-ти удобно использовать для док-ва расходимости послед-ти.
16. Определение предела функции по Коши.
Пусть на E задана ф-я y=f(x) и a – предел точки мн-ва Е. Число А назыв. пределом ф-и f(x) при стремлении x к a, если для любого сколь угодно малого положительного числа ε найдется такое положительное число ƃ(ε), что выполняется неравенство |f(x)-A|<ε лишь только при 0<|x-a|<ƃ и обозначается: 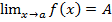 ó (
ó ( ε>0)(Ǝƃ(ε)>0)(
ε>0)(Ǝƃ(ε)>0)( xϵE, 0<|x-a|<ƃ): |f(x)-A|<ε.
xϵE, 0<|x-a|<ƃ): |f(x)-A|<ε.
0<|x-a|<ƃ ó a- ƃ<x<a+ ƃ
a≠x
|f(x)-A|< ε => - ε<f(x)-A< ε |+A => A- ε<f(x)<A+ ε
ƃ (ε) = min{ƃ1, ƃ2}
x находится в малой ƃ-окр-ти точки a, а соответствующие значения ф-и лежат в малой ε-окр-ти А.
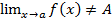 ó (Ǝ ε0>0)(
ó (Ǝ ε0>0)( ƃ>0)(Ǝ
ƃ>0)(Ǝ 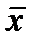 ϵE, 0<|
ϵE, 0<| 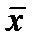 -a|<ƃ): |f(
-a|<ƃ): |f(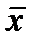 )-A|≥ε0.
)-A|≥ε0.
Определение предела функции по Гейне.
Пусть на Е задана ф-я f(x) и a-предельная точка мн-ва Е. составим из эл-тов мн-ва Е послед-ть значений x: x1, x2, …, xn, …, отличных от a и сходящихся к a.(xn→a, x≠a)( nϵN)
nϵN)
Рассмотрим соответствующую послед-ть значений ф-и f(x1), f(x2), …, f(xn), …. Число А назыв. пределом ф-и f(x) при стремлении x к a, если для любых послед-тей xncE, отличных от a и сходящихся к а, соответствующая послед-ть значений ф-и имеет своим пределом число А. ( {x}cE,xn→a, xn≠a):f(xn)→A.
{x}cE,xn→a, xn≠a):f(xn)→A.
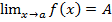 ó Ǝ
ó Ǝ 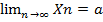
Ǝ 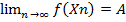
Теорема об эквивалентности двух определений предела.
Опред. Предела по Коши и по Гейне эквивалентны.
Док-во: пусть выполнено определение предела по Коши ( ε>0)(Ǝƃ(ε)>0)(
ε>0)(Ǝƃ(ε)>0)( xϵE, 0<|x-a|<ƃ): |f(x)-A|<ε (1).
xϵE, 0<|x-a|<ƃ): |f(x)-A|<ε (1).
Покажем, что опред. предела по Гейне также будет выполнено. Для этого выберем послед-ть значений x: x1, x2, …, xn, которая сходится к a и и не равна a.(xn→a, x≠a). Это возможно, т.к. а-предельная точка мн-ва Е.
Т.к. 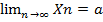 => (
=> ( ƃ=ƃ(ε)>0)(Ǝ N(ε)ϵN)(
ƃ=ƃ(ε)>0)(Ǝ N(ε)ϵN)( nϵN, n> N(ε)):|xn-a|<ƃ.
nϵN, n> N(ε)):|xn-a|<ƃ.
Тогда при  n> N(ε) => |f(xn)-A|<ε в силу определения (1), т.е. получено след. опред.:
n> N(ε) => |f(xn)-A|<ε в силу определения (1), т.е. получено след. опред.:
( ε>0)(ƎN(ε)ϵN)(
ε>0)(ƎN(ε)ϵN)( nϵN, n>N(ε)):|f(xn)-A|<ε =>
nϵN, n>N(ε)):|f(xn)-A|<ε => 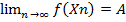 . Это означает, что выполнено определение предела по Гейне.
. Это означает, что выполнено определение предела по Гейне.
Пусть выполняется определение предела по Гейне, т.е. ( {x}cE,xn→a, xn≠a):f(xn)→A. (2) и предположим, что определение предела по Коши не выполнено, т.е. (Ǝ ε0>0)(
{x}cE,xn→a, xn≠a):f(xn)→A. (2) и предположим, что определение предела по Коши не выполнено, т.е. (Ǝ ε0>0)( ƃ>0)(Ǝ
ƃ>0)(Ǝ 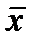 ϵE, 0<|
ϵE, 0<| 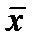 -a|<ƃ): |f(
-a|<ƃ): |f(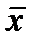 )-A|≥ε0 (3)
)-A|≥ε0 (3)
Т.к. в определении (3) ƃ-любое, то выберем ƃ= ƃn=  , а в качестве
, а в качестве 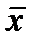 выберем xn из опред. (2)
выберем xn из опред. (2)
Получаем 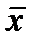 = x1, т.е. 0<|x1-a|< ƃ1=1 => |f(x1)-A|≥ε0
= x1, т.е. 0<|x1-a|< ƃ1=1 => |f(x1)-A|≥ε0
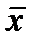 = x2, т.е. 0<|x2-a|< ƃ2=
= x2, т.е. 0<|x2-a|< ƃ2=  => |f(x2)-A|≥ε0
=> |f(x2)-A|≥ε0
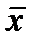 = xn, т.е. 0<|xn-a|< ƃn=
= xn, т.е. 0<|xn-a|< ƃn=  => |f(xn)-A|≥ε0 => при ƃn→∞, ƃn=
=> |f(xn)-A|≥ε0 => при ƃn→∞, ƃn=  →0 =>xn→a, но f(xn) не→А, т.е. определение предела по Гейне не выполнено. Следовательно они эквивалентны.
→0 =>xn→a, но f(xn) не→А, т.е. определение предела по Гейне не выполнено. Следовательно они эквивалентны.
17. Пустьна мн-ве Е задана ф-я y=f(x) и x=a-предельная точка мн-ва Е
Опред.1: число А назыв. правосторонним пределом ф-и а(ч)(пределом ф-и справа) в точке а, если ( ε>0)(Ǝƃ(ε)>0)(
ε>0)(Ǝƃ(ε)>0)( xϵE, a<x<a+ƃ): |f(x)-A|<ε и обозначается A=f(a+0)=
xϵE, a<x<a+ƃ): |f(x)-A|<ε и обозначается A=f(a+0)= 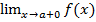 =
= 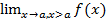 .
.
Опред.2:число А называется левосторонним пределом ф-и а(ч)(пределом ф-и слева) в точке а, если ( ε>0)(Ǝƃ(ε)>0)(
ε>0)(Ǝƃ(ε)>0)( xϵE, a-ƃ <x<a): |f(x)-A|<ε и обозначается A=f(a-0)=
xϵE, a-ƃ <x<a): |f(x)-A|<ε и обозначается A=f(a-0)= 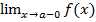 =
= 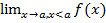 .
.
Необходимое и достаточное условие существования предела ф-и.
Для того, чтобы ф-я имела своим пределом число А при стремлении х к а, необх. и достат., чтобы существовали односторонние пределы в т. а и они были равны между собой
Ǝ f(a-0), f(a+0), f(a-0)=f(a+0)=A
Док-во: 1) необх. Пусть 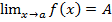 , т.е. выполнено опред.1 (
, т.е. выполнено опред.1 ( ε>0)(Ǝƃ(ε)>0)(
ε>0)(Ǝƃ(ε)>0)( xϵE, 0<|x-a|<ƃ): |f(x)-A|<ε. Здесь 0<|x-a|<ƃ => a-ƃ<x<a+ƃ
xϵE, 0<|x-a|<ƃ): |f(x)-A|<ε. Здесь 0<|x-a|<ƃ => a-ƃ<x<a+ƃ
x≠a
т.е. определение (1) выполнено при a-ƃ<x<a и a<x<a+ƃ =>Ǝ 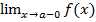 =A и Ǝ
=A и Ǝ 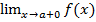 =A => f(a-0)=f(a+0)=A
=A => f(a-0)=f(a+0)=A
2) достат. Пусть Ǝ 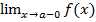 =A и Ǝ
=A и Ǝ 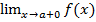 =A ó (
=A ó ( ε>0)(Ǝƃ1(ε)>0)(
ε>0)(Ǝƃ1(ε)>0)( xϵE, a- ƃ1< <x<a): |f(x)-A|<ε (2)
xϵE, a- ƃ1< <x<a): |f(x)-A|<ε (2)
( ε>0)(Ǝƃ2(ε)>0)(
ε>0)(Ǝƃ2(ε)>0)( xϵE, a<x<a+ƃ2): |f(x)-A|<ε (3)
xϵE, a<x<a+ƃ2): |f(x)-A|<ε (3)
Выберем ƃ(ε)=min{ƃ1(ε), ƃ2(ε)}/ тогда при a-ƃ<x<a и a<x<a+ƃ определения (2) и (3) выполн. одновременно. Это означает, что Ǝ 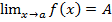 .
.
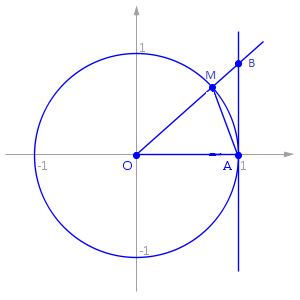 18. Первый замечательный предел.
18. Первый замечательный предел.
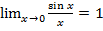
Док-во: пусть 0<x< 
Sтр aom < Sсект aom< Sтр aob
Sтр aom=1/2*om*oa*sinx = 1/2sinx
Sсект aom=(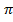 *om2)/2
*om2)/2 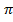 = 1/2*x
= 1/2*x
Sтр aob=1/2*oa*ab=1.2*tgx
1/2sinx < 1/2*x < 1.2*tgx=1/2* 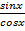 |/ 1/2sinx
|/ 1/2sinx
1 < 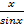 <
< 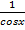 (*) => cosx <
(*) => cosx < 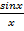 < 1 |*
< 1 |* 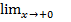 =>по милицейской теореме
=>по милицейской теореме 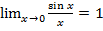
Рассмотрим предел при –  <x<0
<x<0
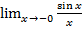 = (замена x=-t, x→0, t→+0) =
= (замена x=-t, x→0, t→+0) = 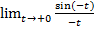 =
= 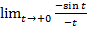 =
= 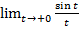 = 1
= 1
Ǝf(+0)=f(-0)=1 => Ǝ 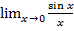
Следствия из первого замечательного предела.
1) Если в (*) перейти
 2015-10-22
2015-10-22 1169
1169