Суть способа состоит во введении новой дополнительной плоскости проекций П3 перпендикулярной одной из исходных плоскостей (либо П1 либо П2). Заданные геометрические фигуры ортогонально проецируют на новую плоскость проекций.
Рассмотрим схему построения чертежа на примере проецирования точки А на дополнительную плоскость П3 ⊥ П1 (рис. 5.1,а).
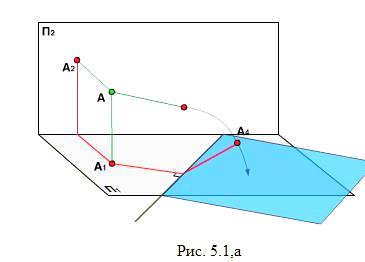 Прямую пересечения новой плоскости П3 с исходной П1 принимаем за новую ось проекции. Вращением на 90° вокруг новой оси П1/П3 совмещаем новую плоскость проекций П3 с плоскостью П1 на первом этапе. Затем на втором этапе совмещаем эти объединенные плоскости с плоскостью П2 поворотом на 90° вокруг оси П2/П1 Можно сказать, что в этом случае плоскость чертежа совмещается с фронтальной плоскостью проекций П2.
Прямую пересечения новой плоскости П3 с исходной П1 принимаем за новую ось проекции. Вращением на 90° вокруг новой оси П1/П3 совмещаем новую плоскость проекций П3 с плоскостью П1 на первом этапе. Затем на втором этапе совмещаем эти объединенные плоскости с плоскостью П2 поворотом на 90° вокруг оси П2/П1 Можно сказать, что в этом случае плоскость чертежа совмещается с фронтальной плоскостью проекций П2.
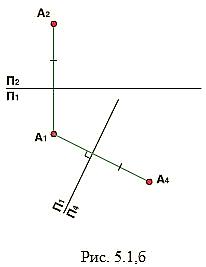 Алгоритм построения чертежа точки (рис. 5.1,б):
Алгоритм построения чертежа точки (рис. 5.1,б):
1) Проводим ось проекций П1/П3;
2) Строим новую линию проекционной связи из точки A1 перпендикулярную оси П1/П3;
3) Откладываем от точки Пересечения новой линии проекционной связи с осью П1/П3 высоту точки A (аппликату Z), равную расстоянию от A2 до старой оси П1/П2
14. Способ вращения вокруг оси, перпендикулярной к плоскости проекций. Геометрическую фигуру вращают вокруг оси, перпендикулярной плоскости проекций, так, чтобы получить частное положение относительно тех же плоскостей проекций. Этот способ для решения некоторых задач более удобен, чем способ замены плоскостей проекций.
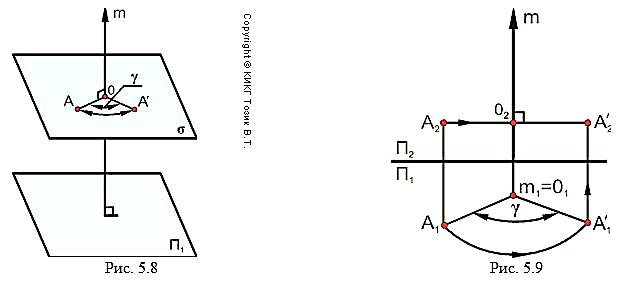
Рассмотрим свойства чертежа на примере вращения точки А вокруг оси m, перпендикулярной П1 (рис. 5.8). Согласно закону вращения, точка А поворачивается вокруг оси m в плоскости s, которая перпендикулярна оси m по дуге окружности, центр которой О принадлежит оси вращения m (О m) на угол поворота g. Поскольку m ⊥ П1, а s m, то s ǁ П1.
Свойства чертежа (рис. 5.9):
1) Первая проекция точки А перемещается по дуге окружности с центром в точке О1 = m1, в которую проецируется ось вращения m. Радиус вращения равен длине отрезка (АО), а на чертеже (А1О1).
2) Вторая проекция точки А перемещается по прямой s2, перпендикулярной проекции оси вращения m2 (s2 ⊥ m2).
15. Кривые поверхности.
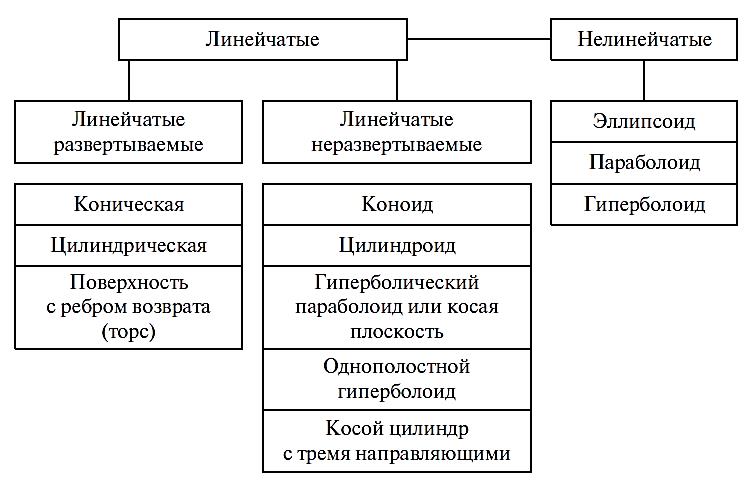
Кривая поверхность – это совокупность всех положений некоторой линии движущейся в пространстве. Движущаяся линия называется образующей поверхности, а линии, определяющие закон ее перемещения, направляющими. Образующая может быть кривой и прямой. Поверхность, образуемая движением прямой линии, называется линейчатой, а движением криволинейной образующей – нелинейчатой поверхностью. Линейчатые поверхности, у которых две соседние образующие параллельны или пересекаются, считают развертываемыми. Остальные линейчатые и все нелинейчатые поверхности — неразвертываемыми.
На рис. 6.1 линейчатая поверхность образована движением прямой образующей l, постоянно проходящей через точку V и во всех своих положениях пересекающей некоторую направляющую m. Эта поверхность называется конической. На рис. 6.2 линейчатая поверхность образована движением образующей l по направляющей m. Такая поверхность называется цилиндрической.
Из нелинейчатых поверхностей рассмотрим поверхности, образованные вращением некоторой линии (образующей) вокруг прямой. Такие поверхности называются поверхностями вращения.
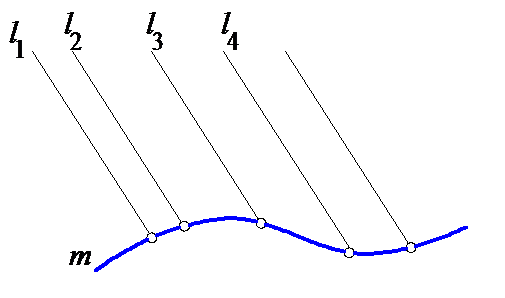
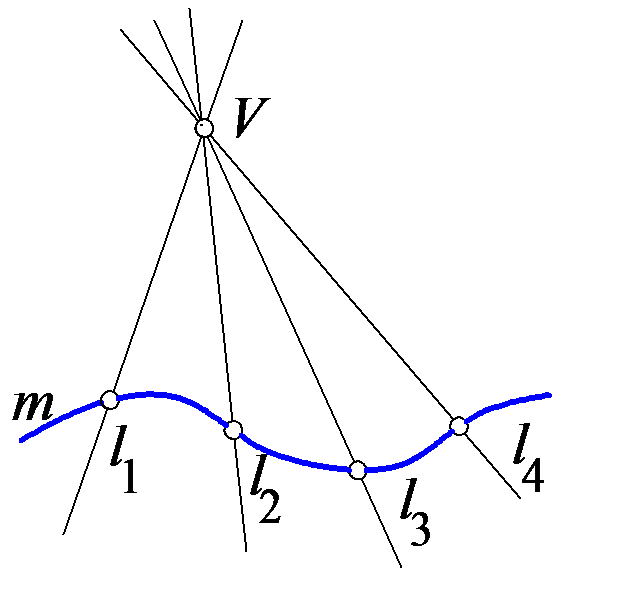
Рис. 6.1 Рис. 6.2
На рис. 6.3 поверхность образована вращением кривой линии l вокруг оси i, лежащей в плоскости этой кривой. Каждая точка М кривой описывает окружность m, называемую параллелью. Параллель наибольшего диаметра называется экватором, наименьшего – горлом. Кривую линию, получающуюся от пересечения поверхности вращения плоскостью, проходящей через ось, называют меридианом. На рис. 6.3 меридианом будет образующая кривая l.
Образующая может быть и прямой линией и кривой, плоской и пространственной.
На рис. 6.4 показано образование поверхности, называемой циклической. Она представляет собой совокупность последовательных положений окружности переменного радиуса, центр которой перемещается по некоторой направляющей m.
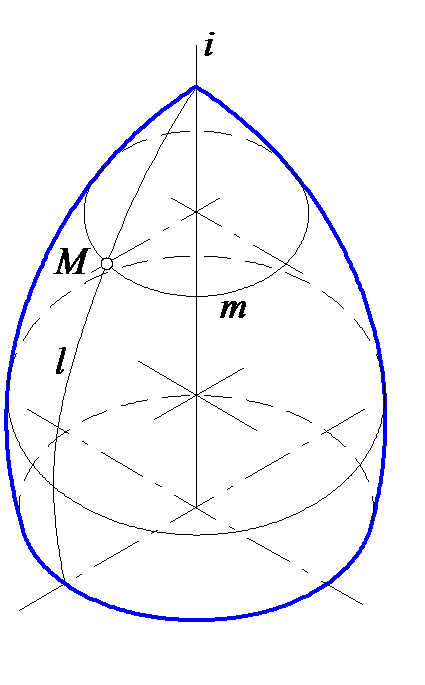
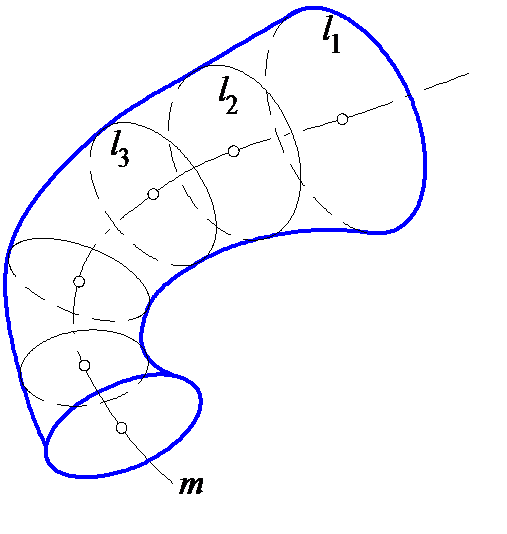
Рис. 6.3 Рис. 6.4
 2015-10-22
2015-10-22 1106
1106
