2015-10-22
1359
Опишем булеву алгебру βn функцией алгебры логики от n переменных. В качестве носителя рассмотрим множество 
. Отношение ≤ на множестве Bn определим по следующему правилу: 
для любого набора значений X=(δ1,…,δn). Пересечением 
называется такая функция h, что h(X)=min{f(X),g(X)} на любом наборе X=(δ1,…,δn). Объединением 
называется такая функция h, чтоh=max{f(X),g(X)} на любом наборе X. Дополнение функции f определяется следующим образом: 
. В качестве 0 рассмотрим функцию, являющуюся константой 0, а в качестве 1 возьмем константу 1. Система 
образует булеву алгебру функций от n переменных (алгебру булевых функций).
Рассмотрим множество B0={0,1} и определим на нем операции 
согласно таблицам истинности. Тогда система 
является двухэлементной булевой алгеброй. Формулы алгебры логики, содержащие лишь логические операции являются термами в β0. По теореме о функциональной полноте в булевой алгебре с помощью терма можно задать любую булеву функцию.
Обозначим через Фn множество всех формул алгебры логики с переменными из множества {x1,…,xn}. На множестве Фn определены двухместные операции конъюнкции и дизъюнкции и одноместная операция отрицания. Выделим на множестве Фn две константы 
и 
. Получается алгебра формул 
. Отношение ≈ эквивалентности формул является конгруенцией на алгебре множестве Фn/≈ операции 
определяются следующим образом: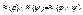 
, 
, 
. На множестве Фn/≈ выделяются две константы: 
и 
. Полученная система 
является фактор-алгеброй Fn/≈.
|
|
|
Теорема: Фактор-алгебра Fn/≈ изоморфна алгебре булевых функций βn.
Доказательство: Искомый изоморфизм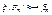 
определяется по следующему правилу: классу эквивалентности ≈(φ) сопоставляется функция fφ, имеющая таблицу истинности произвольной формулы из множества ≈(φ). Поскольку разным классам эквивалентности соответствуют различные таблицы истинности, отображение ξ инъективно, а так как для любой булевой функции f из Bn найдется формула 
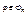, представляющая функцию f, то отображение ξ сюръективно. Сохранение операций 
при отображении ξ проверяется непосредственно.
