Алгеброй Буля называется множество элементов произвольной природы 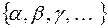 , в котором определены две бинарные операции, назовем их, условно, сложение и умножение и обозначим
, в котором определены две бинарные операции, назовем их, условно, сложение и умножение и обозначим 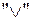 и
и 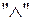 , и одна унарная операция, обозначим ее
, и одна унарная операция, обозначим ее 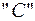 .
.
Введенные операции должны удовлетворять следующим аксиомам:
1) коммутативность:
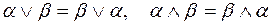 ;
;
2) ассоциативность:
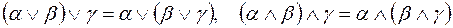 ;
;
3) взаимная дистрибутивность:
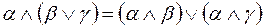 ,
,
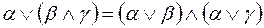 ;
;
4) идемпотентность:
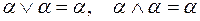 ;
;
5) инволюция:
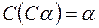 ;
;
6) правила де Моргана:
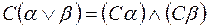 ,
,
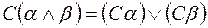 .
.
Кроме введенных операций в алгебре Буля должны существовать два особых элемента, назовем их условно 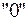 и
и 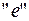 , подчиняющиеся требованиям:
, подчиняющиеся требованиям:
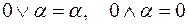 ,
,
 ,
,
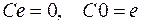 .
.
Алгебру Буля составляет множество 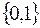 , где 0 и 1 являются логическими переменными (булевыми переменными), с введенными бинарными операциями дизъюнкция и конъюнкция и унарной операцией черта, выделенными элементами являются 0 и 1:
, где 0 и 1 являются логическими переменными (булевыми переменными), с введенными бинарными операциями дизъюнкция и конъюнкция и унарной операцией черта, выделенными элементами являются 0 и 1: 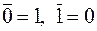 .
.
Алгебру Буля составляет множество подмножеств 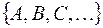 произвольного множества
произвольного множества 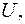 с введенными операциями объединение, пересечение и дополнение:
с введенными операциями объединение, пересечение и дополнение: 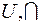 и
и  .Выделенными элементами являются пустое множество
.Выделенными элементами являются пустое множество 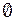 и само множество
и само множество 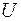 :
:
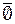
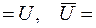
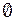 ,
,
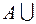
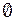
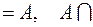
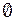 =
= 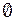 ,
,
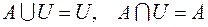 .
.
Название «булева алгебра» связано с именем английского математика Джорджа Буля, хотя полное формальное представление булевой алгебры было дано лишь в 1904 году Хантингтоном.
Задачи
1. Построив таблицу истинности, проверить равенства:
1) 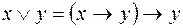 ;
;
2) 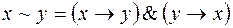 ;
;
3) 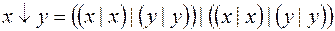 ;
;
4) 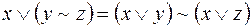 ;
;
5) 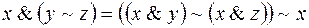 ;
;
6) 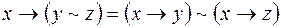 ;
;
7) 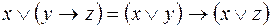 ;
;
8) 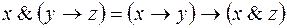 ;
;
9) 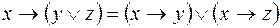 ;
;
10) 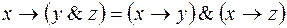 ;
;
11) 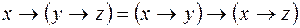 .
.
2. Построить таблицы истинности соответствующих функций, выяснить эквивалентны ли формулы  и
и 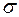 :
:
1) 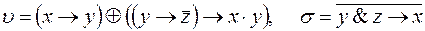 ;
;
2) 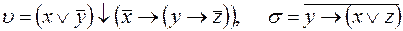 ;
;
3) 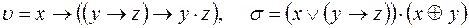 ;
;
4) 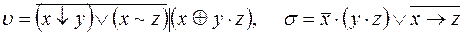 ;
;
5) 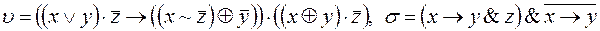 ;
;
6) 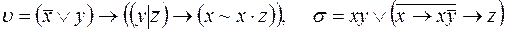 ;
;
7) 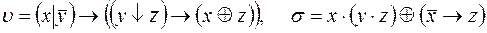 ;
;
8) 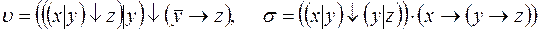 ;
;
9) 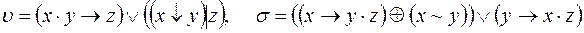 ;
;
10) 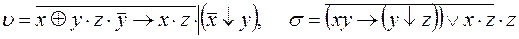 .
.
3. Проверить эквивалентность формул 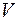 и
и 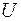 с помощью эквивалентных преобразований:
с помощью эквивалентных преобразований:
1) 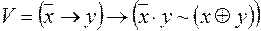 ,
, 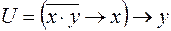 ;
;
2) 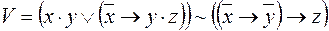 ,
, 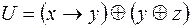 ;
;
3) 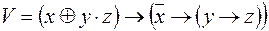 ,
, 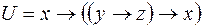 ;
;
4) 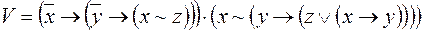 ,
,
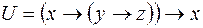 ;
;
5) 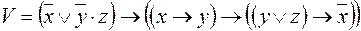 ,
, 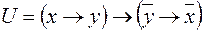 ;
;
6) 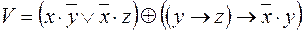 ,
, 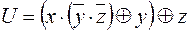 ;
;
7) 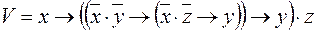 ,
, 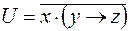 ;
;
8) 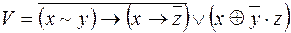 ,
, 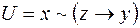 ;
;
9) 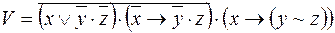 ,
,
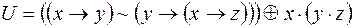 ;
;
10) 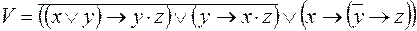 ,
, 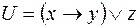 ;
;
4. Используя непосредственно определение двойственности булевых функций, а также основные эквивалентности и соотношения, выяснить, является ли функция g двойственной к функции f:
1) 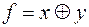 ,
, 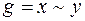 ;
;
2) 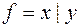 ,
, 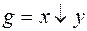 ;
;
3) 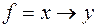 ,
, 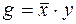 ;
;
4) 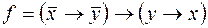 ,
, 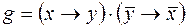 ;
;
5) 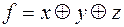 ,
, 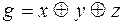 ;
;
6) 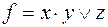 ,
, 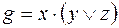 ;
;
7) 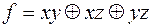 ,
, 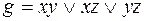 ;
;
8) 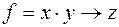 ,
, 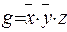 ;
;
9) 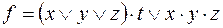 ,
, 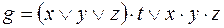 ;
;
10) 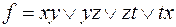 ,
, 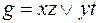 ;
;
11) 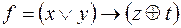 ,
, 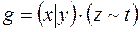 ;
;
12) 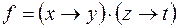 ,
, 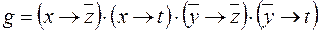 .
.
5. Используя принцип двойственности, построить формулу, реализующую функцию, двойственную к функции f, и проверить, будет ли полученная формула эквивалентна формуле V:
1) 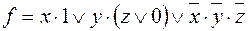 ,
, 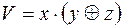 ;
;
2) 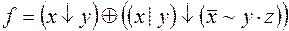 ,
, 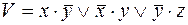 ;
;
3) 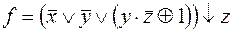 ,
, 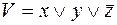 ;
;
4) 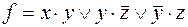 ,
, 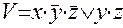 ;
;
5) 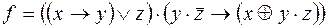 ,
, 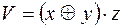 ;
;
6) 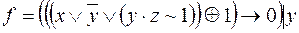 ,
, 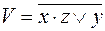 ;
;
7) 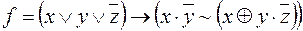 ,
, 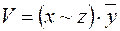 ;
;
8) 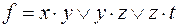 ,
, 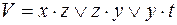 ;
;
9) 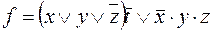 ,
, 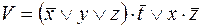 ;
;
10) 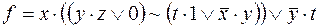 ,
, 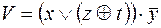 .
.
6. Указать все фиктивные переменные у функции f:
1) 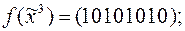
2) 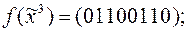
3) 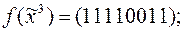
4) 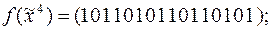
5) 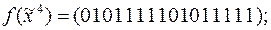
6) 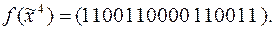
7. Показать, что x 1 – фиктивная переменная у функции f (реализовав для этой цели функцию f формулой, не содержащей явно переменную x 1):
1) 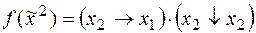 ;
;
2) 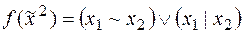 ;
;
3) 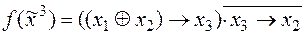 ;
;
4) 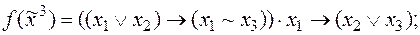 5)
5) 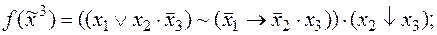 6)
6) 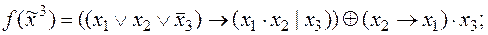 7)
7) 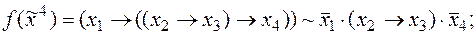
8) 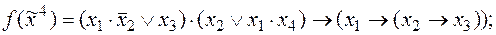 9)
9) 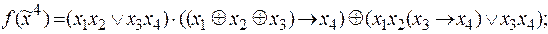 10)
10) 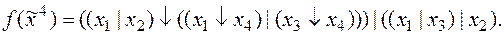
8. Представить в СДНФ следующие функции:
1) 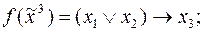
2) 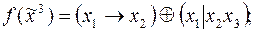
3) 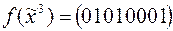 ;
;
4) 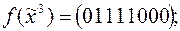
5) 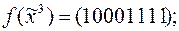
6) 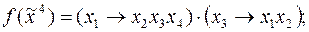
7) 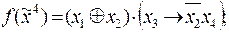
8) 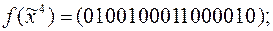
9) 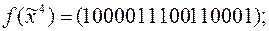
10) 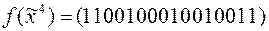 .
.
9. Представить в СКНФ следующие функции:
1) 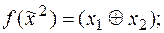
2) 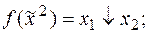
3) 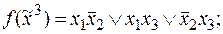
4) 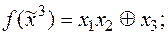
5) 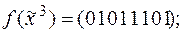
6) 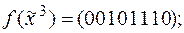
7) 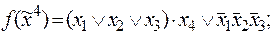
8) 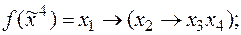
9) 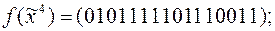
10) 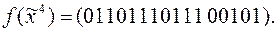
10. С помощью эквивалентных преобразований построить ДНФ функции 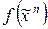 :
:
1) 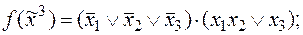
2) 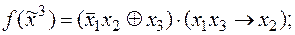
3) 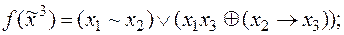
4) 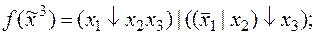
5) 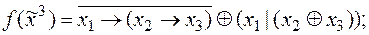
6) 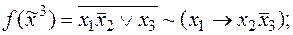
7) 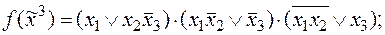
8) 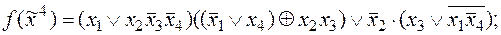
9) 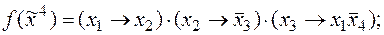
10) 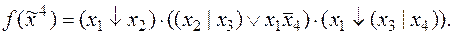
11. Используя эквивалентные преобразования, построить КНФ функции 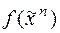 :
:
1) 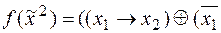
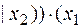
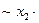
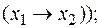
2) 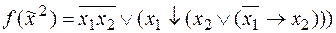 ;
;
3) 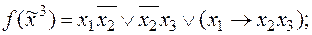


4) 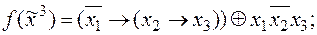
5) 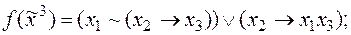
6) 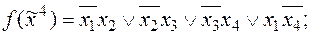
7) 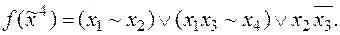
12. Применяя преобразования вида 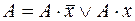 и
и 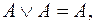 построить из заданной ДНФ функции
построить из заданной ДНФ функции 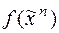 ее совершенную ДНФ:
ее совершенную ДНФ:
1) 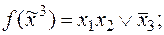
2) 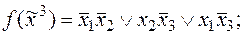
3) 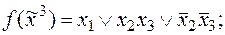
4) 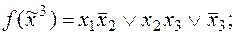
5) 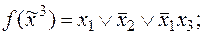
6) 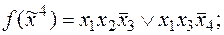
7) 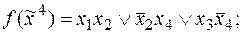
8) 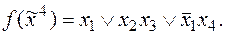
13. С помощью преобразований вида 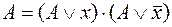 и
и 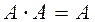 построить из данной КНФ функции
построить из данной КНФ функции 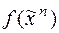 ее совершенную КНФ:
ее совершенную КНФ:
1) 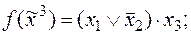
2) 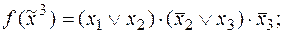
3) 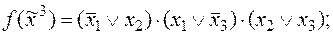
4) 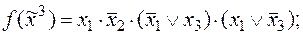
5) 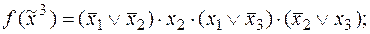
6) 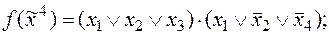
7) 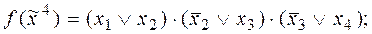
8) 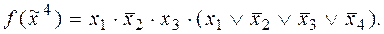
14. Используя дистрибутивный закон 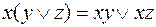 и эквивалентности
и эквивалентности 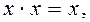
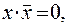
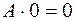 ,
, 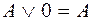 и
и 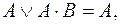 перейти от заданной КНФ функции
перейти от заданной КНФ функции 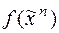 к ДНФ:
к ДНФ:
1) 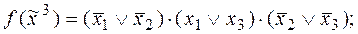
2) 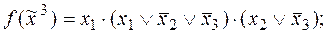
3) 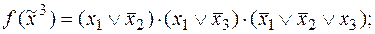
4) 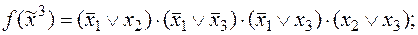
5) 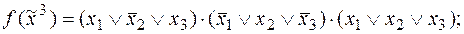
6) 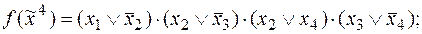
7) 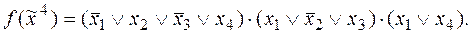
15. Используя дистрибутивный закон 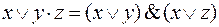 и эквивалентности
и эквивалентности 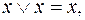
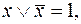
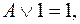
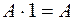 и
и 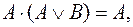 перейти от заданной ДНФ функции
перейти от заданной ДНФ функции 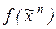 к ее КНФ:
к ее КНФ:
1) 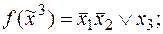
2) 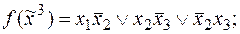
3) 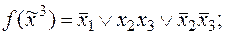
4) 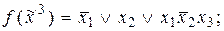
5) 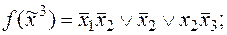
6) 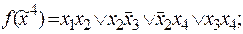
7) 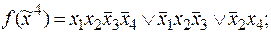
8) 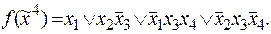
16. Методом неопределенных коэффициентов найти полиномы Жегалкина для следующих функций:
1) 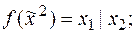 | 6) 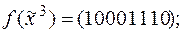 |
2) 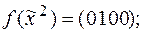 | 7) 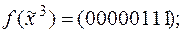 |
3) 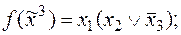 | 8) 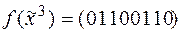 . . |
4) 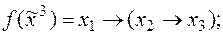 | 9) 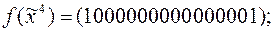 |
5) 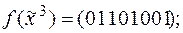 | 10) 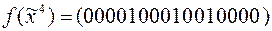 . . |
17. Методом треугольника Паскаля построить полином Жегалкина для следующих функций:
1) 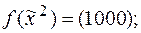 2)
2) 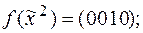
3) 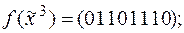 4)
4) 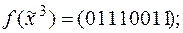
5) 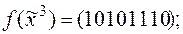 6)
6) 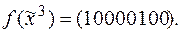
7) 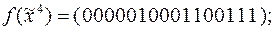 8)
8) 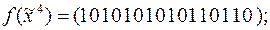
9) 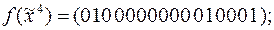 10)
10) 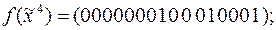
18. Представив функцию 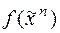 формулой над множеством связок {&,
формулой над множеством связок {&,  }, преобразовать полученную формулу в полином Жегалкина функции
}, преобразовать полученную формулу в полином Жегалкина функции 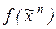 (используя эквивалентности
(используя эквивалентности 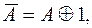
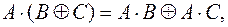
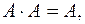
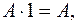
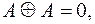
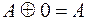 ):
):
1) 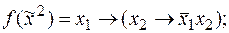
2) 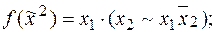
3) 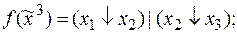
4) 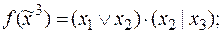
5) 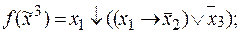
6) 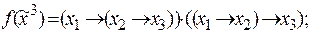
7) 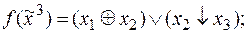
8) 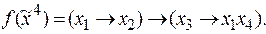
9) 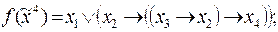
10) 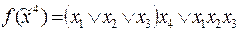 .
.
19. Выяснить, является ли функция 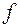 самодвойственной:
самодвойственной:
1) 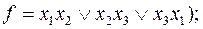
2) 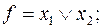
3) 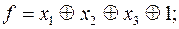
4) 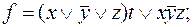
5) 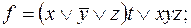
6) 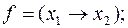
7) 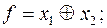
8) 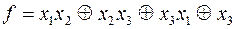 ;
;
9) 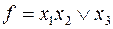 ;
;
10) 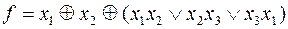 ;
;
11) 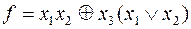 ;
;
12) 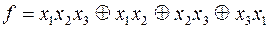 ;
;
13) 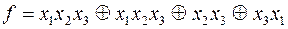 ;
;
14) 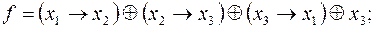
15) 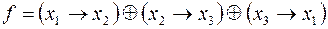 .
.
20. Выяснить, является ли самодвойственной функция 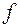 , заданная векторно:
, заданная векторно:
1) 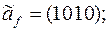
2) 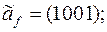
3) 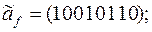
4) 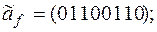
5) 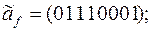
6) 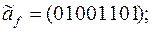
7) 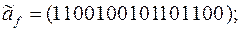
8) 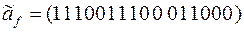 ;
;
9) 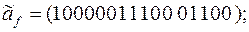
10) 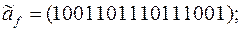
11) 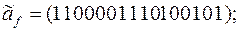
12) 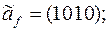
13) 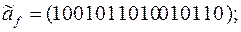
14) 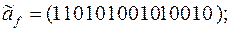
15) 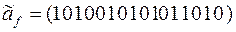 .
.
21. Представив функцию f полиномом, выяснить, является ли она линейной:
1) 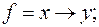
2) 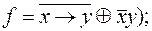
3) 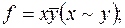
4) 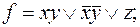
5) 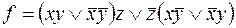 ;
;
6) 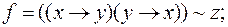
7) 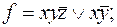
8) 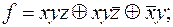
9) 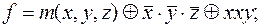
10) 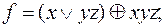
11) 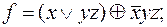
12) 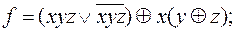
13) 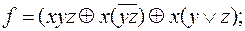
14) 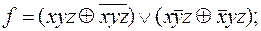
15) 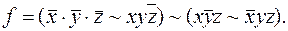
22. Выяснить, является ли линейной функция 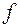 , заданная
, заданная
векторно:
1) 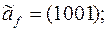
2) 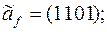
3) 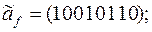
4) 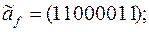
5) 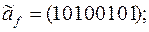
6) 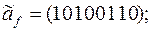
7) 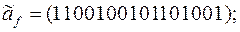
8) 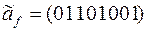 ;
;
9) 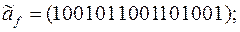
10) 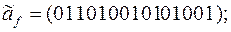
11) 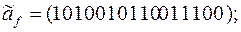
12) 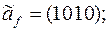
13) 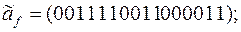
14) 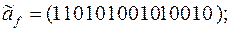
15) 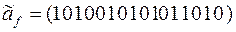 .
.
23. Выяснить, принадлежит ли функция f множеству 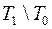 :
:
1) 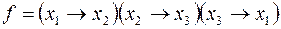 ;
;
2) 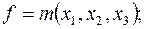
3) 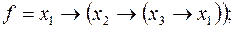
4) 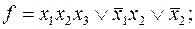
5) 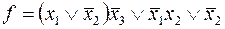 ;
;
6) 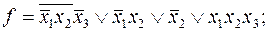
7) 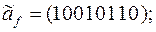
8) 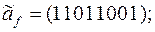
9) 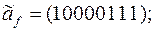
10) 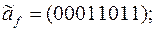
24. Подсчитать число функций, зависящих от переменных 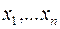 и принадлежащих множеству
и принадлежащих множеству 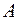 :
:
1) 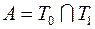 ; 3)
; 3) 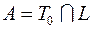 ; 5)
; 5) 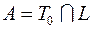 ;
;
2) 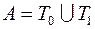 ; 4)
; 4) 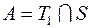 ; 6)
; 6) 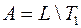 ;
;
7) 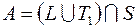 ; 27)
; 27) 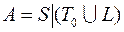 ;
;
8) 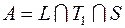 ; 28)
; 28) 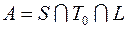 ;
;
9) 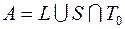 ; 29)
; 29) 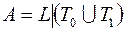 ;
;
10) 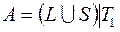 ; 30)
; 30) 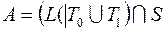 ;
;
11) 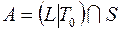 ; 31)
; 31) 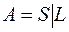 ;
;
12) 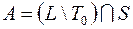 ; 32)
; 32) 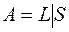 ;
;
13) 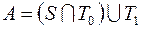 ; 33)
; 33) 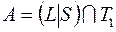 ;
;
14) 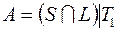 ; 34)
; 34) 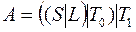 ;
;
15) 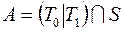 ; 35)
; 35) 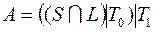 ;
;
16) 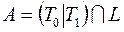 ; 36)
; 36) 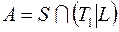 ;
;
17) 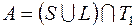 ; 37)
; 37) 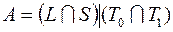 ;
;
18) 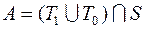 ; 38)
; 38) 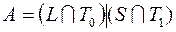 ;
;
19) 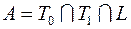 ; 39)
; 39) 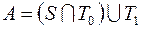 ;
;
20) 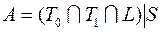 ; 40)
; 40) 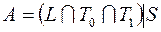 ;
;
21) 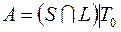 ; 41)
; 41) 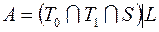 ;
;
22) 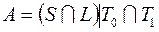 ; 42)
; 42) 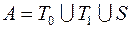 ;
;
23) 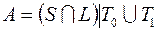 ; 43)
; 43) 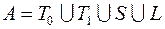 ;
;
24) 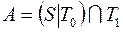 ; 44)
; 44) 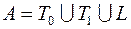 ;
;
25) 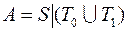 ; 45)
; 45) 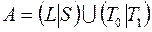 .
.
26) 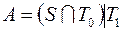 ;
;
25. Доказать, что:
1) 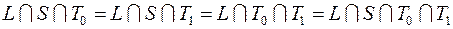 ;
;
2) 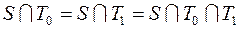 .
.
26. По вектору значений 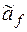 выяснить, является ли функция f монотонной:
выяснить, является ли функция f монотонной:
1) 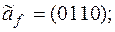
2) 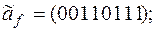
3) 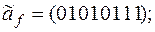
4) 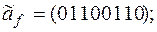
5) 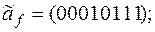
6) 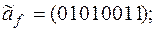
7) 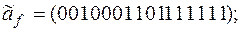
8) 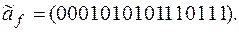
27. Проверить, является ли функция f монотонной:
1) 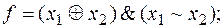
2) 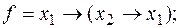
3) 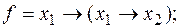
4) 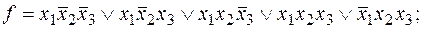
5) 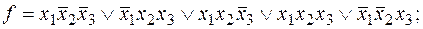
6) 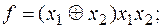
7) 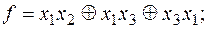
8) 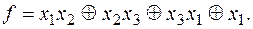
28. Выяснить, полна ли система функций:
1) 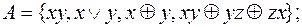
2) 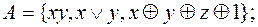
3) 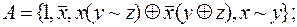
4) 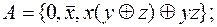
5) 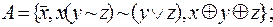
6) 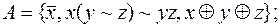
7) 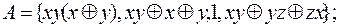
8) 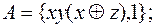
9) 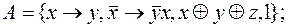
10) 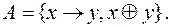
29. Выяснить, полна ли система А функций, заданных векторами своих значений:
1) 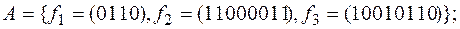
2) 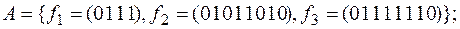
3) 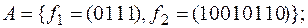
4) 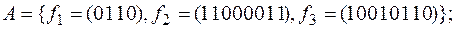
5) 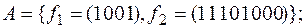
6) 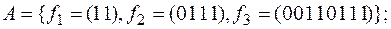
7) 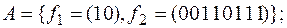
8) 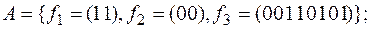
9) 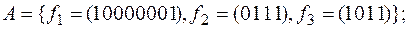
10) 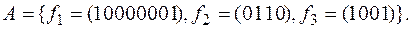
30. Выяснить, полна ли система А:
1) 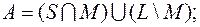
2) 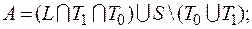
3) 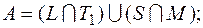
4) 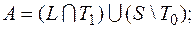
5) 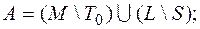
6) 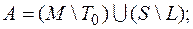
7) 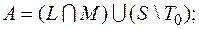
8) 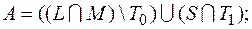
9) 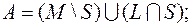
10) 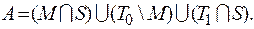
31. Проверить, является ли система функций А базисом в Р 2:
1) 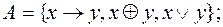
2) 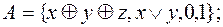
3) 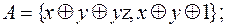
4) 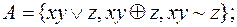
5) 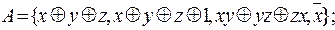
6) 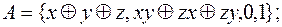
7) 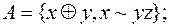
8) 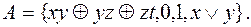
32. Из полной в Р 2 системы А выделить всевозможные базисы:
1) 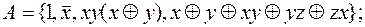
2) 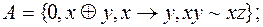
3) 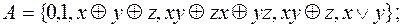
4) 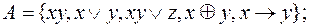
5) 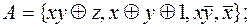
6) 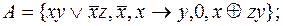
7) 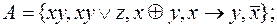
8) 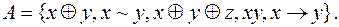
33. Выяснить, можно ли расширить до базиса в 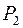 множество
множество 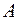 :
:
1) 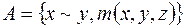 ; 5)
; 5) 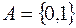 ;
;
2) 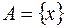 ; 6)
; 6) 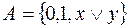 ;
;
3) 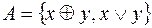 ; 7)
; 7) 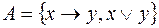 ;
;
4) 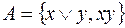 ; 8)
; 8) 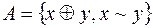 .
.
34. Выяснить, полна ли система функций 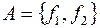 :
:
1) 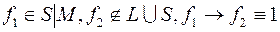 ;
;
2) 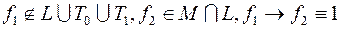 ;
;
3) 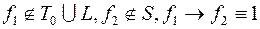 ;
;
4) 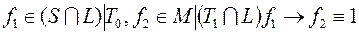 .
.
 2015-05-20
2015-05-20 1147
1147
