ТЕМА: АЛГЕБРА БУЛЯ. БУЛЕВЫ ФУНКЦИИ. ПРИЛОЖЕНИЯ АЛГЕБРЫ ЛОГИКИ В ТЕХНИКЕ.
ПЛАН:
1. Алгебра Буля.
2. Функции алгебры логики.
3. Представление произвольной функции в виде формулы алгебры логики.
4. Приложения алгебры логики в технике (релейно – контактные схемы).
Главная
1. Алгебра Буля.
Равносильности III группы говорят о том, что алгебра логики обладает коммутативными и ассоциативными законами относительно операций конъюнкции и дизъюнкции и дистрибутивным законом конъюнкции относительно дизъюнкции, эти же законы имеют место и в алгебре чисел. Поэтому над формулами алгебры логики можно производить те же преобразования, которые проводятся в алгебре чисел (раскрытие скобок, заключение в скобки, вынесение за скобки общего множителя).
Но в алгебре логики возможны и другие преобразования, основанные на использовании равносильностей:
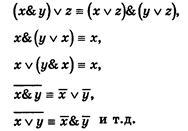
Эта особенность позволяет прийти и к далеко идущим обобщениям.
Рассмотрим непустое множество М элементов любой природы { х, у, г,... }, в котором определены отношение «=» (равно) и три операции: «+» (сложение), «×» (умножение) и «-» (отрицание), подчиняющиеся следующим аксиомам:
Коммутативные законы:
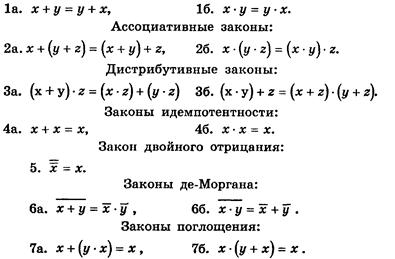
Такое множество М называется булевой алгеброй.
Если под основными элементами х, у, г,... подразумевать высказывания, под операциями «+», «×», «-» дизъюнкцию, конъюнкцию, отрицание соответственно, а знак равенства рассматривать как знак равносильности, то, как следует из равносильностей I, II и III групп, все аксиомы булевой алгебры выполняются.
В тех случаях, когда для некоторой системы аксиом удается подобрать конкретные объекты и конкретные соотношения между ними так, что все аксиомы выполняются, говорят, что найдена интерпретация (или модель) данной системы аксиом.
Значит, алгебра логики является интерпретацией булевой алгебры. Алгебра Буля имеет и другие интерпретации. Например, если под основными элементами х, у, г,... множества М подразумевать множества, под операциями «+», «×», «-» объединение, пересечение, дополнение соответственно, а под знаком равенства - знак равенства множеств, то мы приходим к алгебре множеств. Нетрудно убедиться, что в алгебре множеств, все аксиомы алгебры Буля выполняются.
Среди различных интерпретаций булевой алгебры имеются интерпретации и технического характера. Одна из них будет рассмотрена ниже. Как будет показано, она играет важную роль в современной автоматике.
- Функции алгебры логики.
Как уже отмечалось, значение формулы алгебры логики полностью зависит от значений входящих в эту формулу высказываний. Поэтому формула алгебры логики является функцией входящих в нее элементарных высказываний.
Например, формула 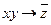 является функцией трех переменных f(x, у, z). Особенностью этой функции является то обстоятельство, что ее аргументы принимают одно из двух значений: ноль или единицу, и при этом функция также принимает одно из двух значений: ноль или единицу.
является функцией трех переменных f(x, у, z). Особенностью этой функции является то обстоятельство, что ее аргументы принимают одно из двух значений: ноль или единицу, и при этом функция также принимает одно из двух значений: ноль или единицу.
Определение. Функцией алгебры логики п переменных (или функцией Буля) называется функция п переменных, где каждая переменная принимает два значения: 0 и 1, и при этом функция может принимать только одно из двух значений: 0 или 1.
Тождественно истинные и тождественно ложные формулы алгебры логики представляют собой постоянные функции, а две равносильные формулы выражают одну и ту же функцию.
Выясним, каково число функций n переменных. Очевидно, каждую функцию алгебры логики (как и формулу алгебры логики) можно задать с помощью таблицы истинности, которая будет содержать 2n строк. Следовательно, каждая функция n переменных принимает 2n значений, состоящих из нулей и единиц. Таким образом, функция nпеременных полностью определяется набором значений из нулей и единиц длины 2n.Общее же число наборов, состоящих из нулей и единиц, длины 2n равно 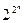 . Значит, число различных функций алгебры логики n переменных равно
. Значит, число различных функций алгебры логики n переменных равно 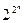 .
.
В частности, различных функций одной переменной четыре, а различных функций двух переменных шестнадцать. Выпишем все функции алгебры логики одной и двух переменных.
Рассмотрим таблицу истинности для различных функций одной переменной. Она имеет вид:
| x | f1(x) | f2(x) | f3(x) | f4(x) |
Из таблицы следует, что f1(x) º 1, f4(x) º 0, f2(x) º x, 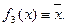
Таблица истинности для всевозможных функций двух переменных имеет вид:
| x | y | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 | f16 |
Аналитические выражения этих функций могут быть записаны следующим образом:
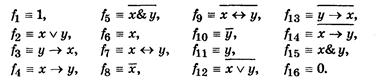
3. Представление произвольной функции алгебры логики в виде формулы алгебры логики.
Пусть F(x1, x2, …, xn) - произвольная функция алгебры логики п переменных. Рассмотрим формулу

которая составлена следующим образом: каждое слагаемое этой логической суммы представляет собой конъюнкцию, в которой первый член является значением функции F при некоторых определенных значениях переменных x1, x2, …, xn,остальные же члены конъюнкции представляют собой переменные или их отрицания. При этом под знаком отрицания находятся те и только те переменные, которые в первом члене конъюнкции имеют значение 0.
Вместе с тем формулаэта содержит в виде логических слагаемых всевозможные конъюнкции указанного вида.
Данная формула полностью определяет функцию F(x1, x2, …, xn). Иначе говоря, значения функции Fи формулы совпадают на всех наборах значений переменных x1, x2, …, xn.
Например, если x 1 принимает значение 0, а остальные переменные принимают значение 1, то функция F принимает значение F(0,1,1,...1). При этом логическое
слагаемое 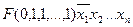 входящее в формулу, принимает также значение F(0,1,...1), все остальные логические слагаемые формулыимеют значение 0. Действительно, в них знаки отрицания над переменными распределяются иначе, чем в рассмотренном слагаемом, но тогда при замене переменных теми же значениями в конъюнкцию войдет символ 0 без знака отрицания, символ 1 под знаком отрицания. В таком случае один из членов конъюнкции имеет значение0, а поэтому вся конъюнкция имеет значение 0. В связи с этим на основании равносильности х v 0 º х значением формулы является.F(0,l,...,l).
входящее в формулу, принимает также значение F(0,1,...1), все остальные логические слагаемые формулыимеют значение 0. Действительно, в них знаки отрицания над переменными распределяются иначе, чем в рассмотренном слагаемом, но тогда при замене переменных теми же значениями в конъюнкцию войдет символ 0 без знака отрицания, символ 1 под знаком отрицания. В таком случае один из членов конъюнкции имеет значение0, а поэтому вся конъюнкция имеет значение 0. В связи с этим на основании равносильности х v 0 º х значением формулы является.F(0,l,...,l).
Ясно, что вид формулыможет быть значительно упрощен, если в ней отбросить те логические слагаемые, в которых первый член конъюнкции имеет значение0 (и, следовательно, вся конъюнкция имеет значение 0).Если же в логическом слагаемом первый член конъюнкции имеет значение1, то, пользуясь равносильностью 1& х º х, этот член конъюнкции можно не выписывать.
Таким образом, в результате получается формула,которая содержит только элементарные переменные высказывания и обладает следующими свойствами:
1) Каждое логическое слагаемое формулы содержит
все переменные, входящие в функцию F(x1, x2, …, xn).
2) Все логические слагаемые формулы различны.
3) Ни одно логическое слагаемое формулы не содержит одновременно переменную и ее отрицание.
4) Ни одно логическое слагаемое формулы не содержит одну и ту же переменную дважды.
Из приведенных рассуждении видно, что каждой не тождественно ложной функции соответствует единственная формула указанного вида.
Если функция F(x1, x2, …, xn) задана таблицей истинности, то соответствующая ей формула алгебры логики может быть получена следующим образом:
для каждого набора значений переменных, на котором функция F(x1, x2, …, xn) принимает значение1, запишем конъюнкцию элементарных переменных высказываний, взяв за член конъюнкции хк,если значение хк на указанном наборе значений переменных есть 1 и отрицание 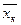 ,если значение хк есть 0. Дизъюнкция всех записанных конъюнкций и будет искомой формулой.
,если значение хк есть 0. Дизъюнкция всех записанных конъюнкций и будет искомой формулой.
Пусть, например, функция F(x1, x2, х3) имеет следующую таблицу истинности:
| x1 | x2 | x3 | F(x1, x2, x3) |
Для наборов значений переменных, на которых функция принимает значение 1составим дизъюнкцию соответствующих конъюнкций:
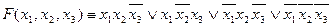 .
.
 2014-02-12
2014-02-12 6542
6542
