1. Диофантовы уравнения.
Решите диофантово уравнение 903x + 994 y = 14
Сначала найдём наибольший общий делитель коэффициентов в левой части, то есть НОД (903, 994).
Применим алгоритм Евклида.
994 = 903 ∙ 1 + 91
903 = 91 ∙ 9 + 84
91 = 84 ∙ 1 + 7
84 = 7 ∙ 12
Таким образом, НОД (903, 994) = 7.
Разделим обе части уравнения 903x + 994 y = 14 на 7.
Получим 129 x + 142 y = 2.
Найдём пару целых чисел x и y, таких, что 129 x + 142 y = 1.
Для этого воспользуемся обобщённым алгоритмом Евклида.
Сначала найдём НОД (129, 142) (мы уже знаем, что он равен 1, но результаты вычислений понадобятся нам для промежуточных выкладок).
142 = 129 ∙ 1 + 13
129 = 13 ∙ 9 + 12
13 = 12 ∙ 1 + 1
12 = 1 ∙ 12
Теперь эти выкладки рассматриваем от конца к началу, то есть выразим 1 как линейную комбинацию 13 и 12, затем – как линейную комбинацию 129 и 13, и, наконец, как линейную комбинацию 142 и 129.
1 = 13 – 12 = 13 – (129 – 13 ∙ 9) = 13 – 129 + 13 ∙ 9 = 13 ∙ 10 – 129 = (142 - 129) ∙ 10 – 129 = 142 ∙ 10 – 129 ∙11
Итак, мы нашли  и
и  такие, что
такие, что  .
.
Но, поскольку уравнение имеет вид 129 x + 142 y = 2, то два найденных числа умножим на 2, то есть в качестве частного решения возьмём  и
и 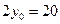 .
.
Теперь найдём общее решение. Если в уравнении 129 x + 142 y = 2 величину x уменьшить на 142, а величину y увеличить на 129, то сумма не изменится, поскольку величина 129 ∙ 142 к одному слагаемому прибавляется, а из другого слагаемого вычитается.
Поэтому можем общее решение записать так.
x = -22 – 142 t, y = 20 + 129 t, t – произвольное целое число.
Это и будет ответом.
Ответ. x = -22 – 142 t, y = 20 + 129 t, t – произвольное целое число.
Примечание 1.
Если в условии стоит не сумма, а разность, например, 129 x – 142 y = 2, то величины
142 t и 129 t нужно будет брать с одним знаком, поскольку в этом случае увеличение чисел 129 x и 142 y будет происходить на одно и то же число. Поэтому их разность не изменится.
Примечание 2.
В этой задаче, как и во многих других задачах данной серии, можно проверить свой ответ, подставив числа в исходное уравнение или в уравнение 129 x + 142 y = 2 (если вы уверены, что правильно сократили).
Подставим их.
129(-22 – 142 t) + 142 (20 + 129 t) = 129 ∙ (-22) – 129 ∙ 142 t + 142 ∙ 20 + 142 ∙ 129 t =
129 ∙ (-22) + 142 ∙ 20 = 2.
При этом, если вы не учли примечание 1 и ошиблись со знаками, то при проверке это сразу увидите.
2. Вычислите 3/19 в кольце вычетов по модулю 35.
Сначала найдём 1/19 в кольце вычетов по модулю 35. Обратите внимание, что мы практически должны вычислить дробь для выражения с целыми числами!
Запишем формулировку задачи так.
x = 1/19 (mod 35)

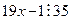
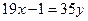
И, наконец: найти целые числа x и y такие, что:
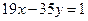 (причём x должен быть одним из остатков при делении на 35, то есть лежать в пределах от 0 до 34 включительно).
(причём x должен быть одним из остатков при делении на 35, то есть лежать в пределах от 0 до 34 включительно).
Подобную задачу мы уже решали – это диофантово уравнение, только достаточно получить одну пару целых чисел, удовлетворяющую условию, а затем заменить полученный x остатком от его деления на 35.
Применим сначала алгоритм Евклида для чисел 19 и 35, затем обобщённый алгоритм Евклида.
35 = 19 ∙ 1 + 16
19 = 16 ∙ 1 + 3
16 = 3 ∙ 5 + 1
3 = 1 ∙ 3
Теперь выразим 1 = НОД (19, 35) в виде линейной комбинации чисел 19 и 35.
1 = 16 – 3 ∙ 5 = 16 – (19 – 16) ∙ 5 = 16 ∙ 6 – 19 ∙ 5 = (35 – 19) ∙ 6 – 19 ∙ 5 = 35 ∙ 6 – 19 ∙ 11.
Итак, при поиске решения уравнения 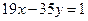 мы получили x = -11.
мы получили x = -11.
Поскольку x должен быть одним из остатков при делении на 35, мы должны заменить -11 остатком от деления на 35. Тогда получим число 24. Это число равно 1/19 в кольце вычетов по модулю 35.
Наконец, вспомним, что мы искали значение 3/19. Для этого умножим число 24 на 3 и разделим результат на 35 с остатком. Получим число 2.
Ответ: 2.
Примечание.
Ответ в этой задаче легко проверить. В самом деле, если мы умножим число 2 на 19, получим число 38, что сравнимо с 3 по модулю 35. То есть 19 x ≡ 3 (mod 35), а, значит,
x = 3/19 в кольце вычетов по модулю 35.
3. Китайская теорема об остатках.
Найти наименьшее натуральное число, которое при делении на 3 даёт остаток 2, при делении на 5 остаток 3, при делении на 7 остаток 2.
Представим искомое число в виде суммы трёх чисел:
одно кратно 5 и 7 и даёт остаток 2 при делении на 3 (поскольку сравнение  имеет решение, похожее сравнение было разобрано в задаче 2),
имеет решение, похожее сравнение было разобрано в задаче 2),
второе кратно 3 и 5 и даёт остаток 2 при делении на 7 (по аналогичной причине),
третье кратно 7 и 3 и даёт остаток 3 при делении на 5.
Первое число будет равно 35, второе равно 30, третье равно 63. Сумма этих чисел равна 128.
Обратите внимание, что это не наименьшее число, дающее требуемые остатки, что не удивительно, при вычислениях мы использовали только величины остатков.
Чтобы получить минимальное число, нужно разделить наш промежуточный результат 128 на произведение чисел 3, 5 и 7, то есть на число 105. Остаток равен 23, это и есть ответ. Проверьте, что он действительно даёт требуемые остатки.
Ответ: 23.
Примечание. Именно в такой формулировке, с этими числами, была разобрана эта задача в самом древнем из дошедших до нас источников – китайском сочинении III века н.э. Поэтому соответствующая теорема называется китайской теоремой об остатках.
4. Системы счисления.
Решите уравнение, записанное в 9-ичной системе счисления.
5 x + 120 = 532
Решение запишите в 9-ичной и десятичной системах счисления.
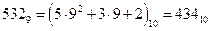
(Это означает, например, что 500 в 9-ичной системе равно  , поскольку число 9 в 9-ичной системе играет ту же роль, что число 10 в десятичной системе счисления).
, поскольку число 9 в 9-ичной системе играет ту же роль, что число 10 в десятичной системе счисления).
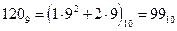
Далее вычисляем в десятичной системе.
5 x = 434 – 99 = 335
x = 335: 5 = 67 (в десятичной системе).
x = 
Ответ: 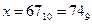
5. Найти представление рационального числа 343/155 непрерывной дробью.

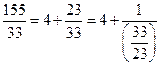
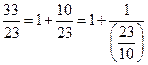

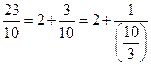
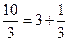
Как только в знаменателе получили целое число, можем собрать все результаты в одну многоэтажную дробь.

Обычно такой ответ записывают в виде: (2; 4, 1, 2, 3, 3).
Техника вычислений (в предисловии: указать рекомендации, что считать вручную, а что на калькуляторе или компьютере, а также рекомендации о разделении материала на лекции и семинары).
 2015-10-22
2015-10-22 446
446








