Пусть  - попарно взаимно простые модули (то есть каждые два взаимно просты между собой),
- попарно взаимно простые модули (то есть каждые два взаимно просты между собой), 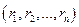 – остатки. Тогда существует такой x, что
– остатки. Тогда существует такой x, что

Вообще говоря, такой x не единственный, поскольку от прибавления к нему величины  остатки по модулю останутся теми же.
остатки по модулю останутся теми же.
Но если поставить дополнительное условие 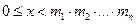 , то такой x существует и единственный.
, то такой x существует и единственный.
Примечание.
То, что модули попарно взаимно просты – существенная деталь. Например, предположим, что 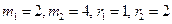 . Тогда искомое число должно быть одновременно и чётным, и нечётным, что невозможно.
. Тогда искомое число должно быть одновременно и чётным, и нечётным, что невозможно.
Сначала, для примера, предположим, что у нас два модуля:  .
.
Тогда представим искомое число в виде суммы двух чисел: одно даёт остаток 1 при делении на 4 и кратно 7, а другое даёт остаток 3 при делении на 7 и кратно 4.
Тогда сумма этих чисел даст искомые остатки.
В качестве первого числа можем взять 21, в качестве второго числа 24. Сложив эти числа, получим 45.
Поскольку для единственности решения поставлено условие  , заменим число 45 его остатком от деления на 28, то есть числом 17.
, заменим число 45 его остатком от деления на 28, то есть числом 17.
Можно проверить, что оно действительно даёт указанные остатки при делении на 4 и на 7.
Теперь - построение решения для китайской теоремы об остатках в общем виде.
Здесь будем строить его похожим образом, то есть в виде суммы n слагаемых, каждое из которых даёт требуемый остаток по своему модулю, и при этом делится на остальные модули.
Первое слагаемое обеспечит остаток по первому модулю, второе – по второму, и так далее.
Обозначим  .
.
Из условия теоремы вытекает, что НОД 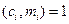
Следовательно, для каждого i существует di такое, что  .
.
Найти такое di можно, если решить сравнение 
(иначе говоря, найти частное решение диофантова уравнения).
Итак, для каждого I выполнено условие  . Поэтому
. Поэтому  .
.
Тогда число 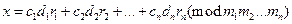 – искомое. Имеется в виду, что мы возьмём остаток от деления данного числа на произведение
– искомое. Имеется в виду, что мы возьмём остаток от деления данного числа на произведение  .
.
В самом деле, это число:
даёт остаток r 1 при делении на m 1 (поскольку первое слагаемое даёт указанный остаток, а остальные слагаемые делятся на m 1),
даёт остаток r 2 при делении на m 2 (поскольку первое слагаемое даёт указанный остаток, а остальные слагаемые делятся на m 2),
и так далее.
 2015-10-22
2015-10-22 2233
2233








