Свойства биномиальных коэффициентов

Доказательство.

Подставим в бином Ньютона a = b = 1.

Доказательство.

Подставим в бином Ньютона a = 1, b = -1.

Шары и перегородки

Рассмотрим задачу: сколько способов представить число n в виде суммы k натуральных слагаемых?

Можно представить её так: набор из n шаров, расположенных в ряд, разделить на k частей, поставив (k-1) перегородок.

В таком виде задача гораздо понятнее, поскольку мы должны выбрать (k-1) мест из (n-1) возможных. А количество сделать это мы знаем - .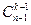

Пример.

Сколько способов представить 10 в виде суммы шести натуральных слагаемых?

Решение.

Представим формулировку в таком виде: разбить цепочку из 10 шаров на шесть групп. Для этого достаточно разместить пять перегородок в 9 промежутках. (НАРИСОВАТЬ!)

Это можно сделать 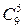способами.

Ответ: .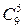

Можно усложнить задачу: сколько способов представить число n в виде суммы k целых слагаемых, каждое из которых не меньше m?

Эту задачу можно свести к предыдущей: для случая m = 1 решать задачу мы умеем, а для общего случая для x_i ≥ m (при i = 1, 2, …, k) можно сделать замену y_i = x_i – m + 1. Получим задачу для чисел y₁, y₂, … y_k, сумму которых мы можем вычислить:

y₁ + y₂ + … + y_k = (x₁ – m + 1) + (x₂ – m + 1) + … + (x_k – m + 1) = (x₁ + x₂ + … + x_k) + k(-m+1) = n – km + k.

Таким образом, все числа y_i натуральные, причём их сумма известна. Такую задачу мы решать уже умеем.

Пример.

Сколько способов представить 100 в виде суммы шести натуральных слагаемых, каждое из которых не меньше 3?

Если каждое из чисел не меньше 1 (то есть натуральное), то способов будет (5 перегородок в 99 промежутков).

Если по условию все , можем сделать замену y_i = x_i – 2, тогда все , то есть получили задачу для суммы натуральных чисел. При этом сумма всех y_i будет на 12 меньше суммы всех x_i, то есть будет равна 100 – 12 = 88.

Итак, получили задачу: сколько способов представить число 88 в виде шести натуральных слагаемых? Такую задачу мы умеем решать. Ответ в данном случае будет равен .

Пример.

Сколько способов представить 100 в виде суммы шести натуральных слагаемых, каждое из которых не меньше -4?

Если по условию все , можем сделать замену y_i = x_i + 5, тогда все , то есть получили задачу для суммы натуральных чисел. При этом сумма всех y_i будет на 30 больше суммы всех x_i, то есть будет равна 100 +30 = 130.

Сколько способов представить число 130 в виде шести натуральных слагаемых?

Ответ: .

Треугольник Паскаля

Рассмотрим задачу, сочетающую правило сложения и нахождение числа сочетаний. Вывести рекуррентную формулу для подсчета биномиальных коэффициентов.

Выделим из n элементов один и разобьем все k-элементные подмножества на два класса:

- содержащие выделенный элемент и

- не содержащие его.

Первых будет 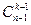, так как один элемент уже выбран, и из оставшихся n-1 элементов надо выбрать еще k-1 элемент.

Вторых будет , так как один элемент запрещается выбирать, и надо выбрать все k элементов из оставшихся n-1.

Так как любое подмножество (сочетание) принадлежит либо одному, либо другому классу и классы не пересекаются, получаем рекуррентную формулу:

Процесс вычислений по этому рекуррентному соотношению можно представить в виде пирамиды, которая называется треугольником Паскаля:

В этом треугольнике каждое число по выведенной рекуррентной формуле есть сумма двух, стоящих над ним, а по границам треугольника стоят единицы.

1 1

1 2 1

1 3 3 1

1 4 6 4 1

………………..

Например, (a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴.