1. Древовидная файловая система, или дерево директорий.
2. Дерево поиска, при котором все потомки с левой стороны всегда меньше родителя, а в правом не меньше.
3. Дерево для вычисления математических формул – например, префиксной и постфиксной формы записи.
Задачи по теме «Деревья»
1. Какое максимальное количество листьев может быть у дерева из n вершин? А минимальное?
2. Могут ли в дереве две вершины соединяться двумя различными путями?
3. Существует ли дерево, у которого одна вершина является и листом, и корнем?
4. Докажите, что в ориентированном дереве у каждой вершины не более одного родителя.
Связные графы
Определение
Если из каждой вершины можно попасть в каждую, то граф отношения называют связным.
Подмножество графа, в котором из каждой вершины можно попасть в каждую, называют компонентой связности.
Из определения можно увидеть, что если граф состоит из одной компоненты связности, он называется связным. Если из более чем одной компоненты связности, он называется несвязным.
Двудольные графы
Определение
Наглядное представление: двудольный граф — это граф, множество вершин которого можно разбить на две части таким образом, что каждое ребро графа соединяет какую-то вершину из одной части с какой-то вершиной другой части, то есть не существует ребра, соединяющего две вершины из одной и той же части.
Определение: неориентированный граф G = (W, E) называется двудольным, если множество его вершин можно разбить на две части  , | U | > 0, | V | > 0, так, что ни одна вершина в U не соединена с вершинами в U и ни одна вершина в V не соединена с вершинами в V.
, | U | > 0, | V | > 0, так, что ни одна вершина в U не соединена с вершинами в U и ни одна вершина в V не соединена с вершинами в V.
Пример: решётка, вершины которой раскрашены в 2 цвета в шахматном порядке.
Двудольный граф называется полным, если для каждой пары вершин  существует ребро
существует ребро  . Для | U | = i, | V | = j такой граф называется Ki , j
. Для | U | = i, | V | = j такой граф называется Ki , j
Упражнение 1. Приведите пример двудольного графа с 6 вершинами.
Упражнение 2. Докажите признаки двудольных графов:
1) Граф является двудольным тогда и только тогда, когда он не содержит цикла нечётной длины.
2) Граф является двудольным тогда и только тогда, когда он 2-раскрашиваем (то есть его хроматическое число равняется двум). Хроматическое число – минимальное количество цветов, требуемое для раскраски вершин графа, при которой любые вершины, соединенные ребром, раскрашены в разные цвета.
Двудольные графы применяются, когда изучаемые объекты разделяются на две группы так, что внутри групп интересующие нас взаимодействия отсутствуют. Например, в экономике — производители и потребители.
На рисунках вершины двудольного графа часто располагают на параллельных прямых.

С двудольными графами связана задача о назначениях. Пусть  — множество претендентов на рабочие места,
— множество претендентов на рабочие места,  — множество рабочих мест. Необходимо каждого из претендентов обеспечить работой в соответствии с его профессиональной подготовкой.
— множество рабочих мест. Необходимо каждого из претендентов обеспечить работой в соответствии с его профессиональной подготовкой.
Булевы функции
Определение. Функцию от одной или нескольких переменных, аргументы и значение которой могут принимать только значения 0 или 1, называют булевой функцией (в честь английского математика Джорджа Буля (1815 - 1864), одного из основателей математической логики).
Примеры.
Конъюнкция:  = 1 тогда и только тогда, когда x и y оба равны 1.
= 1 тогда и только тогда, когда x и y оба равны 1.
Дизъюнкция:  = 1 тогда и только тогда, когда x и y оба равны 1.
= 1 тогда и только тогда, когда x и y оба равны 1.
Для того, чтобы каждый раз не описывать значения словами, булеву функцию обычно задают таблицей истинности, то есть таблицей, в которой указаны значения для всех наборов переменных.
При этом значения наборов переменных располагают в лексикографическом порядке. Сначала набор из одних нулей, затем правый ноль заменяют 1, и так далее, до набора из одних единиц. Например:
| x | y |  |
| x | y |  |
Эквивалентность:  (Значение выражения равно 1, если значения x и y совпадают)
(Значение выражения равно 1, если значения x и y совпадают)
| x | y |  |
Симметрическая разность:  (Значение выражения равно 1, если значения x и y не совпадают)
(Значение выражения равно 1, если значения x и y не совпадают)
| x | y |  |
Импликация:  (Мнемоническое правило: из нуля следует что угодно – и ноль, и единица)
(Мнемоническое правило: из нуля следует что угодно – и ноль, и единица)
| x | y |  |
Отрицание: 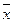
| x | 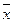 |
 2015-10-22
2015-10-22 1486
1486








