Вычислительные методы линейного программирования

Симплекс-метод. Этот метод является алгебраической формой решения задачи линейного программирования, вытекающей из только что рассмотренного геометрического представления. При обосновании симплекс-метода будем прибегать к уже изложенному выше двухмерному случаю, что позволит достаточно просто перейти от геометрического представления к его алгебраической аналогии.

Первый шаг. Найти допустимый план, соответствующий одной из вершин области допустимых планов.

Второй шаг. Проверить, оптимален ли найденный план. Если оптимален, вычисления окончены. Если нет – следующий план.

Третий шаг. Переход к другой вершине (другому допустимому плану), в которой значение целевой функции меньше, проверка его на оптимальность и так далее.

Поэтому первым шагом должно быть получение координат одной из вершин многоугольника (многогранника) допустимых планов. Для этого необходимо преобразовать систему уравнений таким образом, чтобы с ее помощью можно было легко получить координаты вершины многоугольника (многогранника) области допустимых планов.

Анализируя рис 6.1, можно заметить, что в каждой из вершин две из переменных обращаются в нуль. Поэтому мы должны положить две переменные равными нулю, а затем найти остальные четыре из системы уравнений (6.4.). В совокупности все переменные дадут один из допустимых планов, соответствующих некоторой вершине.

Чтобы преобразовать систему уравнений описанным образом, необходимо выразить каждую из неизвестных через остальные.

Такая возможность существует лишь в случае, если определитель

Если это условие выполняется, то величины называют базисными. Каждый базис соответствует определенной вершине.

Преобразуем систему уравнений (6.4.) так, чтобы, приравнивая две переменные нулю (например, ), можно было получить значения базисных величин — координаты одной из вершин многоугольника.

Предварительно убедимся, что определитель, составленный из коэффициентов при этих неизвестных в уравнениях (6.4.), не равен нулю.

Действительно,

Это дает нам право считать, что величины являются базисными и система (6.4.) может быть разрешена относительно их.

Все необходимые преобразования будем производить с матрицей коэффициентов уравнений (6.4.):

(6.11)

Преобразуем матрицу (6.11.) в соответствии с указанным выше требованием получения базисных значений переменных величин. Для этого необходимо выполнить над ней такие преобразования, чтобы базисные переменные остались по одной в каждом из уравнений (строке матрицы), а коэффициенты при них были равны единице. Начинаем с коэффициента при в первом уравнении. Чтобы сделать его равным единице, делим все коэффициенты первого уравнения на четыре. Для исключения переменной из остальных уравнений отнимаем от каждого из них первое уравнение, умноженное на такое число, при котором разность коэффициентов при была бы равна нулю. Например, второе и третье уравнения (строки) нужно умножить на нуль, четвертое – на единицу.

В результате преобразований получим

Аналогичные преобразования выполняем для переменной во второй строке:

Для переменной — в третьей строке и — в четвертой:

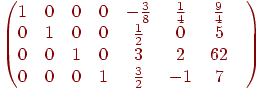(6.12)

Выполненная процедура носит название метода полного исключения (так называемое Жарданово исключение).

Теперь, приравнивая переменные и (соответственно пятый и шестой столбцы матрицы) нулю, можем написать значение базисных переменных, которые будут в этом случае равны свободным членам соответствующих уравнений:

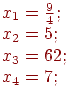
Обращаясь к геометрической интерпретации (рис. 6.1), можно убедиться, что полученные координаты 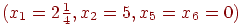соответствуют вершине многоугольника — области допустимых планов. Это и есть первый допустимый план.

Теперь можно перейти ко второму шагу симплекс-метода – установлению того, является ли допустимый план, соответствующий найденной вершине , оптимальным.

Наиболее естественным путем решения этой задачи был бы сплошной перебор всех вершин области допустимых планов, определение для каждой из них значений переменных 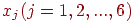и вычисление по ним в каждой вершине величины целевой функции.

Та вершина, в которой величина окажется минимальной, и даст искомый оптимальный план.

Но этот путь весьма неэкономный, ибо требует просчитать большое количество планов, в том числе и явно неоптимальных.

Симплекс-метод предусматривает поэтому не сплошной, а направленный перебор планов, когда каждый последующий план оказывается лучше предыдущего. Число вычислительных операций при этом резко сокращается.

В чем сущность направленного перебора?

В первом допустимом плане, соответствующем вершине , целевая функция в соответствии с формулой (6.7.) равна:

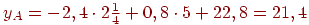
Мы уже знаем из (6.10.), что . Следовательно, целевая функция в точке значительно больше минимума, и необходимо продолжать перебор вершин-планов до тех пор, пока не придем к оптимальному.

Из вершины можно перейти к соседним вершинам и (рис. 6.1), двигаясь по сторонам многоугольника 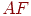и соответственно. Видимо, нужно избрать такое направление перехода к соседней вершине, которое приведет к наибольшему уменьшению целевой функции.

Рассчитаем значения целевой функции для соседних вершин . Пользуясь формулой (6.7.) и подставляя соответствующие значения , , получим:

Сопоставляя два последних выражения, нетрудно убедиться, что минимизация функции цели достигается при движении к точке по стороне . Это означает, что в базис вводится переменная , которая в вершине была равна нулю.

Поскольку при отсутствии наглядного геометрического представления заранее нельзя располагать значениями переменных в вершинах многоугольника, то для установления необходимости и направления перебора планов пользуются специальным критерием :

(6.13)

где индекс приписывается небазисным (нулевым) переменным, а индекс — базисным. Имеется доказательство того, что в случае оптимальности полученного плана все становятся равными нулю или меньшими нуля. Включению в базис подлежит та переменная, для которой принимает наибольшее положительное значение. В нашем примере это:

Таким образом, мы приходим к тому же заключению о необходимости включения в базис переменной , для которой критерий имеет наибольшее положительное значение.

Далее необходимо установить, какая переменная должна быть выведена из базиса при введении в него переменной . Чтобы ответить на этот вопрос, будем рассуждать так.

Очевидно, следует переместиться по стороне как можно дальше от точки , чтобы как можно больше уменьшить целевую функцию. Стало быть, можно взять в качестве координаты точки ее максимальное возможное значение, которое допускается системой уравнений, соответствующей матрице (6.12.), то есть такое, при котором ни одна из переменных не становится отрицательной. Можно показать, что это достигается в том случае, если вывести из базиса переменную, которой соответствует минимальное положительное значение отношения свободного члена уравнения к коэффициенту при в соответствующем столбце матрицы (6.12.).

Поэтому избирается четвертая строка матрицы и соответственно переменная , подлежащая исключению из базиса.

Теперь необходимо получить в четвертой строке значение коэффициента при новой базисной величине , равного единице, а все остальные коэффициенты этого столбца обратить в нуль. Для этого повторяем вычислительную процедуру полного исключения.

Получим

(6.14)

Данной матрице отвечает допустимый план в вершине . Приравнивая небазисные переменные нулю , получаем значения остальных переменных, соответствующих второму плану:

Как уже было показано, 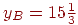. Итак, получено существенное сокращение целевой функции, однако критерий продолжает оставаться положительным, что говорит о необходимости дальнейшего улучшения плана:

На этот раз в базис вводится переменная , а выводится переменная , которой соответствует наименьшее значение коэффициента в столбце .

После преобразования матрицы (6.14.) получаем матрицу (6.15.), отвечающую третьему плану:

(6.15)

Данный план соответствует вершине :

Критерии для данного плана равны:

Поскольку нет ни одного положительного критерия, то третий план и является оптимальным, что следует из рис. 6.1.

Целевая функция при данном плане равна:

Итак, мы пришли аналитическим путем к тому же оптимальному плану, который был ранее получен геометрическим способом.

Решение примера 6.1. можно сформулировать следующим образом.

Чтобы общие потери были минимальны, количество носителей первого типа должно быть равно 4, второго – 0, третьего – 16, четвертого 0, пятого 10, шестого – 8.

При этом потери в носителях будут составлять 13,2 единицы.

Важно отметить, что наихудший план распределения, соответствующий точке , приводит к потерям 26,8 единиц. Таким образом, без дополнительного расходования носителей и овощей (только за счет их рационального распределения) улучшен результат решения задачи перевозки более чем в два раза.

Полученное решение – целочисленное, что, однако, не является обязательным для задач линейного программирования. В ряде случаев для получения целочисленного решения приходится прибегать к искусственным приемам, что существенно усложняет вычислительную процедуру.