Имеется  пунктов поставщиков
пунктов поставщиков 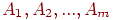 и
и  пунктов назначения (потребителей)
пунктов назначения (потребителей)  .
.
 — количество груза в тоннах, сосредоточенное в пункте
— количество груза в тоннах, сосредоточенное в пункте 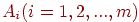 ;
;
 — количество груза, ожидаемое в пункте
— количество груза, ожидаемое в пункте 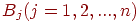 .
.
Принимаем условие
 | (6.16) |
означающее, что суммарный запас груза равен суммарной потребности в нем.
 — стоимость перевозки одной тонны груза из пункта
— стоимость перевозки одной тонны груза из пункта  в пункт
в пункт  .
.
 — количество тон груза, перевезенное из пункта
— количество тон груза, перевезенное из пункта  в пункт
в пункт  .
.
Требуется найти оптимальный план перевозок, то есть рассчитать, сколько груза должно быть отправлено из каждого пункта отправления в каждый пункт назначения, с тем условием, чтобы суммарная стоимость перевозок была наименьшей.
Неизвестными в нашей задаче являются  неотрицательных чисел
неотрицательных чисел 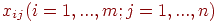 . Сведем их в таблицу 6.1, назовем ее матрицей перевозок.
. Сведем их в таблицу 6.1, назовем ее матрицей перевозок.
| Таблица 6.1. Матрица перевозок | |||||
 |  | ... |  | ||
 |  |  | ... |  |  |
 |  |  | ... |  |  |
| ... | ... | ... | ... | ... | ... |
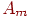 |  |  | ... |  |  |
 |  | ... |  |
Запишем соотношение для пунктов поставщиков 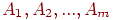 и пунктов потребителей
и пунктов потребителей  .
.
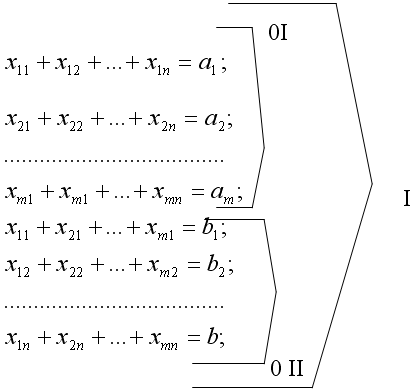
Будем называть уравнение 0I горизонтальными уравнениями, а 0II – вертикальными. Перевозка из  и
и  стоит
стоит  , общая стоимость всех перевозок будет
, общая стоимость всех перевозок будет
 | (II) |
где суммирование производится по всем  и всем
и всем  . Таким образом, мы пришли к следующей задаче линейного программирования:
. Таким образом, мы пришли к следующей задаче линейного программирования:
Дана система уравнений I и линейная функция II. Требуется среди неотрицательных решений системы найти такое, которое минимизирует функцию II.
 2015-10-22
2015-10-22 849
849








