Геометрическая интерпретация задачи линейного программирования

Геометрическую интерпретацию задачи линейного программирования рассмотрим на примере.

Пример

Четыре вида овощей необходимо распределить по шести транспортным средствам .

Распределение овощей по транспортным средствам сопряжено с необходимостью учета ряда ограничений, которые могут быть описаны системой четырех уравнений с шестью неизвестными, аналогичными системе 6.2.

(6.4)

Смысл первого уравнения в нашем примере означает, что овощ типа 1, общий ресурс которого составляет 16 единиц, может размещаться в количестве четырех единиц на транспортном средстве первого типа и одной единицы на транспортном средстве четвертого типа. Аналогично и второе уравнение и так далее.

Последнее условие говорит о том, что число типов транспортного средства не может быть отрицательным.

Необходимо определить, какое количество транспортного средства каждого типа следует иметь, чтобы общие потери в них были минимальными.

Оплата за конкретное транспортное средство (в тысячах рублей) задана следующей таблицей.

Тип единицы транспорта,
Стоимость перевозки на транспорте данного типа,	0,4	0,5	0,2	0,8	0,6	0,3

В соответствии с приведенными данными, целевая функция, подлежащая оптимизации, примет вид:

(6.5)

Решение задачи сводится к выполнению ограничений, заданных уравнением (6.4.)

В этом примере, когда , каждое из ограничительных линейных уравнений (6.4.), а также линейная функция (6.5.), могут быть представлены геометрически в двухмерном пространстве (на плоскости), что дает возможность весьма наглядно интерпретировать основные идеи метода линейного программирования.

Геометрическая интерпретация задачи линейного программирования. Чтобы иметь возможность наглядно представить ограничения и целевую функцию на графике, необходимо выразить все неизвестные через две независимые величины, например, и , соответствующие координатным осям, относительно которых будет производиться построение (рис. 6.1). Из уравнения (6.4.) следует:

(6.6)

А целевая функция примет такой вид:

.

Из сопоставления уравнений (6.6.) и последнего из ограничений (6.2.) следует:

(6.8)

Каждому из неравенств (6.8.) на графике рис. 6.1 соответствует полуплоскость, в пределах которой находятся все допускаемые данным неравенством значения переменной величины .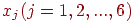

Так, например, неравенству соответствует полуплоскость вправо от оси (граница ее заштрихована).

Неравенству

соответствует полуплоскость вправо и вверх от линии, соответствующей значению данного неравенства (при ).

Уравнение этой линии

.

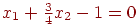Таким же образом можно построить границы, определяемые другими уравнениями.

Неравенствам (6.8.) соответствует некоторая область – шестиугольник , образованный границами упомянутых выше полуплоскостей. Эта область может быть названа областью допустимых планов, поскольку любая точка в ее пределах отвечает требованиям наложенных ограничений (6.4.).

Из всех доступных планов нас интересует оптимальный план, при котором функция цели достигает минимума.

Целевой функции соответствует семейство параллельных прямых. Рассмотрим одну из них, проходящую через начало координат, что будет иметь место при .

При этом

.

Интересующая нас прямая , как видно из рисунка 6.1, имеет наклон вправо от оси . Задаваясь различными значениями , получим семейство прямых линий, параллельных прямой , которая проходит через точку 0. При этом чем меньше будет , тем, очевидно, правее располагается соответствующая прямая.

Поскольку мы добиваемся минимального значения , нас будет интересовать прямая, расположенная в наибольшем удалении вправо от прямой и проходящая через многоугольник , — прямая .

Как видно из рисунка 6.1, единственной точкой, соответствующей оптимальному плану, будет та вершина многоугольника , которая одновременно принадлежит области допустимых планов и отвечает требованию минимизации целевой функции — вершина .

Итак минимум целевой функции достигается в вершине многогранника. Существует теорема о том, что для любой задачи линейного программирования найдется вершина многогранника допустимых решений, в которой целевая функция достигает своего минимального (максимального) значения.

Рис. 6.1.

Общий алгоритм нахождения оптимального плана

Рассмотрим общий путь нахождения оптимального плана на примере.

1. Построить область допустимых планов, соответствующую наложенным ограничениям (6.4.)
2. Найти вершину указанной области, в которой целевая функция минимальна.
3. Найти соответствующие избранной вершине величины переменных, которые и дадут оптимальный план.

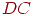Первый шаг в решении задачи – построение области допустимых планов – нами уже сделан (см. рис. 6.1). Из рисунка видно, как определить координаты точки , соответствующей оптимальному плану. Из уравнения прямой , проходящей через ту же точку, следует, что . Из уравнения прямой , проходящей через ту же точку, следует, что . Подставляя полученные значения и в уравнения (6.6.), определим величины остальных переменных, составляющих оптимальный план:

Таким образом, оптимальный план будет следующим:

(6.9)

Линейная форма при этом будет минимальной и равной

(6.10)

Рассмотренная геометрическая интерпретация задачи линейного программирования возможна лишь при наличии двух независимых переменных. При трех переменных наглядное представление существенно усложняется, так как в этом случае имеет место некоторый выпуклый многогранник в трехмерном пространстве, соответствующий объему допустимых планов.

При количестве переменных более трех задача теряет геометрическую наглядность, так как трудно представить себе, например, четырехмерное пространство. Однако идея получения решения, рассмотренного выше, сохраняет смысл и для случая многомерного пространства.

На основе этой идеи создан и разработан один из основных методов решения задач линейного программирования – так называемый симплекс-метод.