В.И. Романовский предложил более простой метод оценки близости эмпирического распределения к нормальному, используя величину  он предложил вычислять отношение
он предложил вычислять отношение
 , где К – число степеней свободы.
, где К – число степеней свободы.
Если это отношение по абсолютной величине меньше трех, то расхождение между эмпирическим и теоретическим распределениями считается несущественным; если же это отношение по абсолютной величине больше трех, то расхождение существенно.
Несущественность расхождения говорит о возможности принять за закон данного эмпирического распределения нормальное распределении.
Применим критерий Романовского к нашей задаче, имеем:
 =
=  ,
, 
то есть расхождение существенно, между эмпирическим и теоретическим распределением в смысле критерия Романовского. Следовательно, надо отвергать гипотезу на уровне 0,95 и брать уровень ниже, например, 0,9, так этот критерий более чувствителен к отклонениям частот, чем критерий Пирсона.
 |
Критерий λ, предложенный А.Н. Колмогоровым, устанавливает близость теоретических и эмпирических распределений путем сравнения их интегральных распределений. λ исчисляется исходя из D – максимума абсолютного значения разности накопленных частот признака, отнесенного к квадратному корню из числа наблюдений.
 , где D -
, где D - 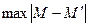 , где
, где  - накопленные эмпирические частоты;
- накопленные эмпирические частоты;
 - накопленные теоретические частоты.
- накопленные теоретические частоты.
Приведем таблицу значений Р(λ), - вероятности того, что λ достигнет данной величины.
| λ | Р(λ) | λ | Р(λ) | |
| 0,30 | 1,0000 | 1,10 | 0,1777 | |
| 0,35 | 0,9997 | 1,20 | 0,1122 | |
| 0,40 | 0,9972 | 1,30 | 0,0881 | |
| 0,45 | 0,9874 | 1,40 | 0,0397 | |
| 0,50 | 0,9639 | 1,50 | 0,0222 | |
| 0,55 | 0,9228 | 1,60 | 0.0120 | |
| 0,60 | 0,8643 | 1,70 | 0,0062 | |
| 0,70 | 0,7112 | 1,90 | 0,0015 | |
| 0,75 | 0,6272 | 2,00 | 0,0007 | |
| 0,80 | 0,5441 | 2,10 | 0,0003 | |
| 0,85 | 0,4653 | 2,20 | 0,0001 | |
| 0,90 | 0,3927 | 2,30 | 0,0001 | |
| 0,95 | 0,3275 | 2,40 | ||
| 1,00 | 0,2700 | 2,50 |
Если найденному значению λ соответствует очень малая вероятность Р(λ) (меньше 0,05), то расхождение между эмпирическим и теоретическим распределением нельзя считать случайным и, таким образом, первое мало отражает второе.. Если Р(λ) – величина значительная (больше 0,05), то расхождение между частотами может быть случайным. И распределения хорошо соответствуют одно другому.
Применяя критерий Колмогорова к нашей задаче, имеем:
Таблица 3.
 |  |  |  |  |  |
| Мах 4 |
D = 4., n = 60,  ≈ 0,52, Р(λ) ≈ 0.9228
≈ 0,52, Р(λ) ≈ 0.9228
 Это большая вероятность (0,9228 > 0,05) указывает на то, что расхождение между эмпирическим и теоретическим распределениями могло быть случайным и можно принять, что закон данного эмпирического распределения – это нормальное распределение в смысле критерия Колмогорова.
Это большая вероятность (0,9228 > 0,05) указывает на то, что расхождение между эмпирическим и теоретическим распределениями могло быть случайным и можно принять, что закон данного эмпирического распределения – это нормальное распределение в смысле критерия Колмогорова.

Критерий Ястремского
В общем виде критерий Б.С. Ястремского можно записать следующим неравенством:
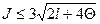 , где
, где 
где  - эмпирические частоты;
- эмпирические частоты;  - теоретические частоты; l – число групп. Для числа групп, меньших 20, Θ = 0,6; q = 1 – p.
- теоретические частоты; l – число групп. Для числа групп, меньших 20, Θ = 0,6; q = 1 – p.
Значение 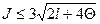 показывает несущественность расхождения между эмпирическими и теоретическими частотами в данном распределении.
показывает несущественность расхождения между эмпирическими и теоретическими частотами в данном распределении.
При значении 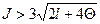 расхождение между эмпирическим и теоретическим распределениями существенно. Применим критерий Ястремского к проверке нашей гипотезы. Таблица расчета величины С.
расхождение между эмпирическим и теоретическим распределениями существенно. Применим критерий Ястремского к проверке нашей гипотезы. Таблица расчета величины С.
Таблица 4.
 |  |  | 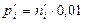 |  |  |  |   |  |
| 0,04 | 0,96 | 3,84 | 4,17 | |||||
| 0,11 | 0,89 | - 1 | 9,79 | 0,10 | ||||
| 0,16 | 0,84 | - 4 | 13,44 | 1,19 | ||||
| 0,16 | 0,84 | - 2 | 13,44 | 0,298 | ||||
| 0,09 | 0,91 | 8,19 | 0,122 | |||||
| 0,04 | 0,96 | 3,84 | 1,041 | |||||
| Σ=60 | Σ=60 | Σ = 6,921 |
С≈6,9; Θ = 0,6; l = 6; 

Получили значение J=0,9 меньше  , следовательно, расхождение между эмпирическими и теоретическими частотами в данном распределении несущественны.
, следовательно, расхождение между эмпирическими и теоретическими частотами в данном распределении несущественны.
 2015-10-22
2015-10-22 3522
3522
