Для построения нормальной кривой выполняют следующее:
1) Находят выборочную среднюю и среднее квадратическое отклонение (методом произведений) в лабораторной работе № 2 нашли эти значения:
 = 167,6,
= 167,6, 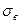 ≈ 9,1
≈ 9,1
2) Вычисляют ординаты  (выравнивающие частоты) теоретической кривой по формуле
(выравнивающие частоты) теоретической кривой по формуле
 , где
, где 

Значение функции  находим по таблице (Приложение 1) значений функции
находим по таблице (Приложение 1) значений функции
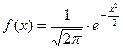 , функция
, функция 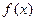 четная, т.е.
четная, т.е. 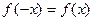
Значение функции  округляют до ближайшего целого числа и принимают за теоретические частоты
округляют до ближайшего целого числа и принимают за теоретические частоты  . Все расчеты записываются в таблицу:
. Все расчеты записываются в таблицу:

Таблица 1.
 | 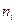 |  |  |  |  |  |
| - 14,6 | - 1,6 | 0,1109 | 4,4 | |||
| - 8,6 | - 0,96 | 0,2516 | 10,8 | |||
| - 2,6 | - 0,29 | 0,3825 | ||||
| 3,4 | 0,3 | 0,3814 | ||||
| 9,4 | 1,03 | 0,2347 | 9,4 | |||
| 15,4 | 1,69 | 0,0957 | 3,84 | |||
Σ 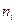 = 60 = 60 | Σ  = 60 = 60 |
3) Строят точки с координатами  в прямоугольной системе координат и соединяют их плавной кривой. Полученная кривая и будет нормальной кривой, построенной по опытным данным.
в прямоугольной системе координат и соединяют их плавной кривой. Полученная кривая и будет нормальной кривой, построенной по опытным данным.
Строим эмпирическую кривую распределения и нормальную (Рис. 1). Близость выравнивающих (теоретических) частот к эмпирическим позволяет предположить, что исследуемый признак распределен нормально.
|
|
|

Рис. 1. Кривые распределения: эмпирическая и теоретическая
Проверим согласованность эмпирического распределения с теоретическим нормальным.
Для этого воспользуемся так называемыми критериями согласия.
Имеется несколько критериев согласия:
критерий Пирсона ( ;
;
критерий Ястремского;
элементарные приемы определения нормальности распределения и т.д.
Критерий Пирсона
Рассмотрим применение критерия  к проверке гипотезы о нормальном распределении генеральной совокупности значений исследуемого признака.
к проверке гипотезы о нормальном распределении генеральной совокупности значений исследуемого признака.
Вычисляем  по формуле
по формуле  ,
,
где 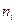 - эмпирические частоты,
- эмпирические частоты,  - теоретические частоты.
- теоретические частоты.
Для оценки того, насколько данное эмпирическое распределение согласуется с теоретическим, вычисляют  . Значение
. Значение  табулировано в зависимости от числа степеней свободы (К) исследуемого признака. Число степеней свободы вычисляют по формуле: К = m – r – 1, где m – число интервалов значений признака (в нашей задаче m=6), r - число используемых статистических характеристик (r=2, т.к. мы использовали
табулировано в зависимости от числа степеней свободы (К) исследуемого признака. Число степеней свободы вычисляют по формуле: К = m – r – 1, где m – число интервалов значений признака (в нашей задаче m=6), r - число используемых статистических характеристик (r=2, т.к. мы использовали 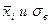 для расчета теоретических частот. Поэтому К = 6 – 2 – 1 = 3.
для расчета теоретических частот. Поэтому К = 6 – 2 – 1 = 3.
Для вычисленных  и К находим вероятность
и К находим вероятность  . Если эта вероятность значительно отличается от нуля (>0,1), то можно считать, что эмпирическое распределение согласуется с теоретическим нормальным (Приложение 2).
. Если эта вероятность значительно отличается от нуля (>0,1), то можно считать, что эмпирическое распределение согласуется с теоретическим нормальным (Приложение 2).
Все расчеты записываются в таблицу:
Таблица 2.
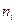 |  |  |  |  |
| - 1 | 0,09 | |||
| - 4 | 1,0 | |||
| - 2 | 0,25 | |||
| 0,1 | ||||
| 1,0 | ||||
| Σ = 60 | Σ = 60 | Σ =6,44 |
 = 6,44,
= 6,44,  ≈ 0,12, так как полученная вероятность значительно отличается от нуля, то можно считать, что эмпирическое распределение согласуется с теоретическим нормальным в смысле критерия Пирсона.
≈ 0,12, так как полученная вероятность значительно отличается от нуля, то можно считать, что эмпирическое распределение согласуется с теоретическим нормальным в смысле критерия Пирсона.
|
|
|
На графике изображена кривая вероятностей по критерию Пирсона. На оси 0х указывается значение  .
.
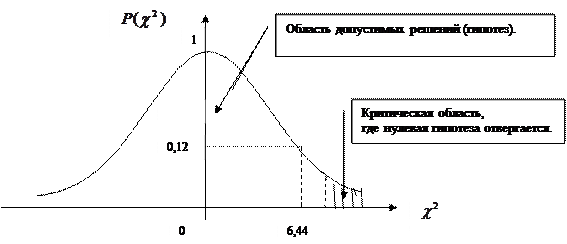 |
Вывод: нулевая гипотеза не отвергается, а принимается с коэффициентом значимости 0,95.
 2015-10-22
2015-10-22 2991
2991
