Методы исследования объектов, динамика которых описывается дифференциальными уравнениями с использованием программы для моделирования
SciLab (MatLab)
Цель занятия:
1. Получить практические навыки исследования систем (объектов), динамика которых описывается дифференциальными уравнениями.
2. Научиться разрабатывать алгоритм и программу с среде моделирования SciLab (MatLab ).
3. Практически усвоить численные методы Эйлера для решения дифференциальных уравнений 1-го и 2-го порядков
Задачи занятия:
1. Разработка алгоритма в виде блок-схемы
2. Построение графиков кривых y(x), dy/dx при параметрах a-const и var.
3. Анализ результатов исследований.
Модели объектов исследования
aӳ+bý + cy=f
1. a,c,f - const, t – var (t0 – tk, h= 0.1, 0.01)
2. a,f - const, t -var(t0 – tk, h= 0.1, 0.01), b- var
Пример 1
Условие задачи:составить алгоритм и проект моделирования объекта, динамика которого описывается дифференциальным уравнением 1 порядка методом Эйлера
ý + 4 ysin(t)-5.
Программа
function yd= f (t, y),yd=5*t-4*y*sin(t),endfunction;
y0=5;t0=0;t=0:0.01:3;
y=ode(y0,t0,t, f);
plot (t,y)

Рис. 20. Результаты исследования
Пример 2
Условие задачи:составить алгоритм и проект моделирования объекта, динамика которого описывается дифференциальным уравнением 1-го порядка методом Эйлера
ý + а* ysin(t)-5, при изменении параметра на 4 значения.
N=4;
//disp(’Vvod N’);
//Цикл для ввода элементов в массиве y.
a=1;a1=2;
for i=1:N
function yd= f (t, y), yd=5*t-a*y*sin(t), endfunction;
y0=5;t0=0;t=0:0.01:3;
y=ode(y0,t0,t, f);
plot (t,y)
a=a+a1;
end
disp(y);

Рис. 21. Результаты исследования
Пример 3
Условие задачи:составить алгоритм и проект моделирования объекта, динамика которого описывается дифференциальным уравнением 2-го порядка методом Эйлера
ӱ + 0.2*ý+ 4*y=2.
function dy= syst (t, y)dy=zeros(2,1);
dy(1)=y(2);
dy(2)=2-0.2*y(2)-4*y(1)
endfunction
y0=[0;0];t0=0;t=0:0.1:5;
y=ode(y0,t0,t, syst);
plot (t,y)
//end
//disp(y);

Рис. 21. Результаты исследования
Пример 4
Условия задачи. Исследовать объект, динамика которого описывается дифференциальным уравнением
ӱ + 0.2*ý+ 4*y=2
методом визуального моделирования
Исходное уравнение преобразуем к виду
Ӱ=2-0.2*ý-4*y
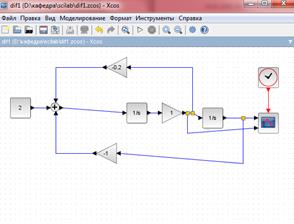
Рис. 22. Визуальная схема моделирования

Рис. 23. Результаты моделирования

Рис. 24. Визуальная схема моделирования

Рис. 25. Результаты моделирования
Пример 5
Условие задачи:составить алгоритм и проект моделирования объекта, динамика которого описывается дифференциальным уравнением 2-го порядка методом Эйлера
ӱ + 0.2*ý+ 4*y=2
N=4;
//disp(’Vvod N’);
//Цикл для ввода элементов в массиве y.
//a=1;a1=5;
//for i=1:N
function dy= syst (t, y)
dy=zeros(2,1);
dy(1)=y(2);
dy(2)=2-0.2*y(2)-4*y(1)
endfunction
y0=[0;0];t0=0;t=0:0.1:5;
y=ode(y0,t0,t, syst);
plot (t,y)
//end
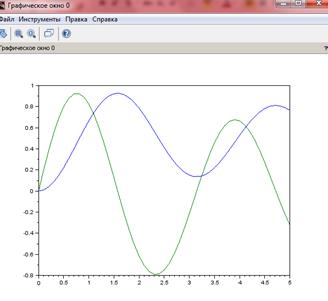
Рис. 25. Результаты моделирования
Пример
 2015-10-22
2015-10-22 1234
1234








