2015-10-22
281
Рассмотрим следующую упрощенную статическую модель распределения тракторных работ (Корбут А.А. Целочисленные задачи линейного программирования. В сб. "Эконом.-матем. методы", вып. 2, М., "Наука", 1965, 141-186.).
Имеется n типов сельскохозяйственных машин и m видов работ, подлежащих выполнению в объемах 
, 
(будем считать, что все эти объемы выражены в гектарах). Заданы производительность 
-й машины на 
-й работе 
, а также себестоимость 
обработки одного гектара работы машиной . Себестоимость самих машин (скажем, стоимость их покупки или аренды, взятая с некоторым коэффициентом приведения) составляет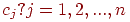 
. Следует найти оптимальный машинный парк для данного комплекса работ и указать его распределение по работам. Чтобы выполнить задание и добиться минимальной суммарной себестоимости, обозначим через 
количество машин каждого типа, а через 
— количество машин типа , которое будет выделено на работу . Тогда наша задача сведется к минимизации
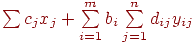
| (7.38) |
при условиях
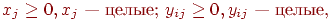
| (7.39) |
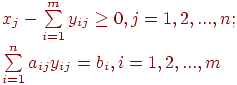
| (7.40) |
Отметим, что накладывать условие целочисленности на не обязательно, так как нецелые здесь вполне поддаются разумной интерпретации.
Таким образом, перед нами еще один пример задачи с неделимостями. Модель эта существенно усложнится, если дополнительно потребовать выполнения каждой работы в отведенные для нее агротехнические сроки; здесь мы не будем на этом останавливаться.
